Many phenomena in engineering and the physical and biological sciences can be described using mathematical models. Frequently the resulting models cannot be solved analytically, in which case a common approach is to use a numerical method to find an approximate solution. The aim of this course is to introduce the basic ideas underpinning computational mathematics, study a series of numerical methods to solve different problems, and carry out a rigorous mathematical analysis of their accuracy and stability.
这是一份UCL伦敦大学学院MATH0033作业代写的成功案
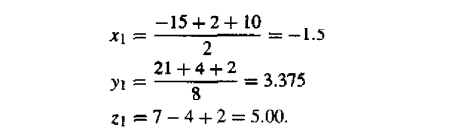
Step 1 . Evaluate the function
$$
\boldsymbol{F}\left(\boldsymbol{p}{k}\right)=\left[\begin{array}{l} f{1}\left(p_{k}, q_{k}\right) \
f_{2}\left(p_{k}, q_{k}\right)
\end{array}\right]
$$
Step 2. Evaluate the Jacobian
$$
\boldsymbol{J}\left(\boldsymbol{P}{k}\right)=\left[\begin{array}{ll} \frac{\partial}{\partial x} f{1}\left(p_{k}, q_{k}\right) & \frac{\partial}{\partial y} f_{\mathrm{I}}\left(p_{k}, q_{k}\right) \
\frac{\partial}{\partial x} f_{2}\left(p_{k}, q_{k}\right) & \frac{\partial}{\partial y} f_{2}\left(p_{k}, q_{k}\right)
\end{array}\right]
$$
Step 3. Solve the linear system
$$
J\left(P_{k}\right) \Delta P=-F\left(P_{k}\right) \text { for } \Delta P
$$
Step 4. Compute the next point:
$$
P_{k+1}=P_{k}+\Delta P .
$$

MATH0033 COURSE NOTES :
$$
f(x)=P_{N}(x)+E_{N}(x),
$$
where $P_{N}(x)$ is a polynomial that can be used to approximate $f(x)$ :
$$
f(x) \approx P_{N}(x)=\sum_{k=0}^{N} \frac{f^{(k)}\left(x_{0}\right)}{k !}\left(x-x_{0}\right)^{k} .
$$
The error term $E_{N}(x)$ has the form
$$
E_{N}(x)=\frac{f^{(N+1)}(c)}{(N+1) !}\left(x-x_{0}\right)^{N+1}
$$
for some value $c=c(x)$ that lies between $x$ and $x_{0}$.