Mathematical models are used extensively in many areas of the Biological Sciences. This course aims to give a sample of the construction and mathematical analysis of such models in Population Ecology. The fundamental question to be addressed is: what natural (or human) factors control the abundance and distribution of the various populations of animals and plants that we see in Nature?
这是一份UCL伦敦大学学院MATH0030作业代写的成功案
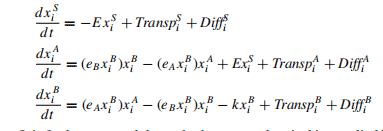

The rate of change in the concentrations of $n$ interacting molecular species $\left(c_{i}, i=1,2, \ldots n\right)$ is determined by their reaction kinetics and expressed in terms of ordinary differential equations
$$
\frac{d c_{i}}{d t}=F_{i}\left(c_{1}, c_{2} \ldots c_{n}\right) .
$$
The explicit form of the functions $F_{i}$ in Eq. (4.1) depends on the details of the reactions. Spatial inhomogeneities also cause time variations in the concentrations even in the absence of chemical reactions. If these inhomogeneities are governed by diffusion, then in one spatial dimension,
$$
\frac{\partial c_{i}}{\partial t}=D_{i} \frac{\partial^{2} c_{i}}{\partial x^{2}} .
$$
Here $D_{i}$ is the diffusion coefficient of the $i$ th species. In general, both diffusion and reactions contribute to the change in concentration and the time dependence of the $c_{i} \mathrm{~s}$ is governed by reaction-diffusion equations
$$
\frac{\partial c_{i}}{\partial t}=D_{i} \frac{\partial^{2} c_{i}}{\partial x^{2}}+F_{i}\left(c_{1}, c_{2} \ldots c_{n}\right) .
$$

MATH0030 COURSE NOTES :
In addition, one can also define the average value of $X$ per vertex, $X_{a}$, as well as its normalized value, $0 \leq X_{n} \leq 1$ :
$$
\begin{array}{r}
X_{a}=\frac{X}{V} ; \quad{ }^{k} X_{a}=\frac{{ }^{k} X}{V} \
X_{n}=\frac{X}{X\left(K_{V}\right)} ; \quad{ }^{k} X_{n}=\frac{{ }^{k} X}{{ }^{k} X\left(K_{V}\right)}
\end{array}
$$