这是一份oxford牛津大学作业代写的成功案例
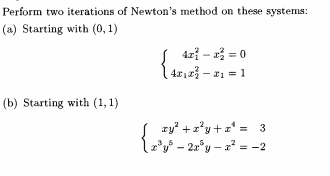
The connection between the homotopy methods and Newton’s method is deeper than may be seen at first glance. Let us start with the homotopy
$$
h(t, x)=f(x)-e^{-t} f\left(x_{0}\right)
$$
In this equation, $t$ will run from 0 to $\infty$. We seek a curve or path, $x=x(t)$, on which
$$
0=h(t, x(t))=f(x(t))-e^{-t} f\left(x_{0}\right)
$$
As usual, differentiation with respect to $t$ will lead to a differential equation describing the path:
$$
\begin{aligned}
0 &=f^{\prime}(x(t)) x^{\prime}(t)+e^{-t} f\left(x_{0}\right) \
&=f^{\prime}(x(t)) x^{\prime}(t)+f(x(t)) \
x^{\prime}(t) &=-\left[f^{\prime}(x(t))\right]^{-1} f(x(t))
\end{aligned}
$$

Oxford COURSE NOTES :
On the other hand,
$$
(P A){\imath \jmath}=\sum{k=1}^{n} P_{\imath k} a_{k \jmath}=\sum_{k=1}^{n} \delta_{p_{1} k} a_{k j}=a_{p_{\imath} j}
$$
Thus we have proved, for all pairs $(i, j)$, that
$$
(P A){i j}=(L U){i j}
$$