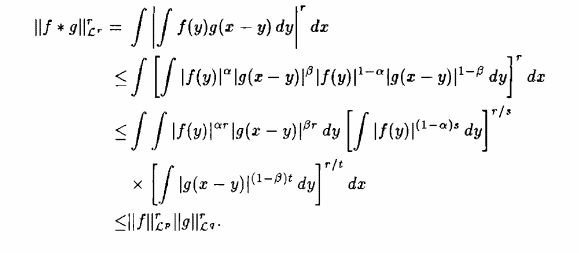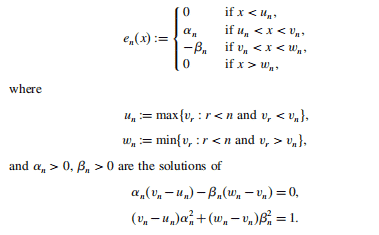

If $\lambda<0$ then
$$
0=\phi_{+}(\lambda f+|\lambda| f)=\phi_{+}(\lambda f)+\phi_{+}(|\lambda| f)=\phi_{+}(\lambda f)+|\lambda| \phi_{+}(f) .
$$
Therefore
$$
\phi_{+}(\lambda f)=-|\lambda| \phi_{+}(f)=\lambda \phi_{+}(f) .
$$
Therefore $\phi_{+}$is a linear functional on $\mathcal{B}$. It is non-negative in the sense defined above.
We define $\phi_{-}$by $\phi_{-}:=\phi_{+}-\phi$, and deduce immediately that it is linear. Since $f \in \mathcal{B}{+}$implies that $\phi{+}(f) \geq \phi(f)$, we see that $\phi_{-}$is non-negative. The boundedness of $\phi_{\pm}$will be a consequence of the boundedness of $|\phi|$ and the formulae
$$
\phi_{+}=\frac{1}{2}(|\phi|+\phi), \quad \phi_{-}=\frac{1}{2}(|\phi|-\phi)
$$

MATH0071 COURSE NOTES :
$$
\int_{a}^{b} f(x) \mathrm{d} x
$$
which is defined by approximating $f$ by piecewise constant functions, for which the definition of the integral is evident. It is easy to show that the integral depends linearly on $f$ and that
$$
\left|\int_{a}^{b} f(x) \mathrm{d} x\right| \leq \int_{a}^{b}|f(x)| \mathrm{d} x
$$
Moreover
$$
\left\langle\int_{a}^{b} f(x) \mathrm{d} x, \phi\right\rangle=\int_{a}^{b}\langle f(x), \phi\rangle \mathrm{d} x
$$