This is a first course at the advanced undergraduate level in mathematical finance; centring on the mathematics of financial derivatives which relies on both probability theory and PDE based approaches. It assumes no prior knowledge of finance. The module begins with an introduction to the type of language and terminology used in the investment banking arena, followed by the essential elements of probability theory and stochastic calculus required for the pricing of options later in the course.
这是一份UCL伦敦大学学院MATH0031作业代写的成功案
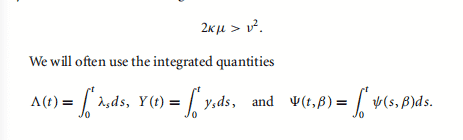

Under the equivalent martingale measure $\mathcal{Q}$, the one-factor Vasicek (1FV) model is given by
$$
d r_{t}=\chi_{r}\left(\bar{r}-r_{t}\right) d t+\sigma_{r} d W_{r, t}^{\mathcal{Q}}
$$
Under this specification bond prices are defined by $D(t, T)=\exp (A(t, T)-$ $\left.B(t, T) r_{t}\right)$, where $B(t, T) \equiv \frac{1-e^{-x_{f} t}}{x_{t}}$,
$$
A(t, T) \equiv \frac{(B(t, T)-\tau)\left(x_{r}^{2} \bar{r}-\frac{\sigma_{r}^{2}}{2}\right)}{x_{r}^{2}}-\frac{\sigma_{r}^{2} B^{2}(t, T)}{4 \chi_{r}}
$$
and, for notational convenience, $\tau \equiv T-t$.
Let $\tilde{X}{t} \equiv\left[y{l, L}(t) r_{t}\right]^{\prime}$ and $\tau_{l} \equiv T_{l}$, the term-to-maturity of the swaptions contract to be priced. The associated transform of the state vector $\tilde{X}{t}$ is given by $$ \psi^{\mathcal{Q}{l+\perp L}}\left(\tilde{u} \equiv(\tilde{u} 0)^{\prime}, \tilde{X}{t}, 0, T{l}\right)=\exp \left[\alpha\left(\tau_{l}\right)+\tilde{u} y_{l, L}(0)\right]
$$

MATH0031 COURSE NOTES :
The one-factor generalized Vasicek (1FGV) model defines the short rate $r_{t}=$ $\delta+x_{1, t}$, where $\delta \in \mathbb{R}$ is constant, and
$$
d x_{1, t}=-x_{1} x_{1, t} d t+\sigma_{1} d W_{1, t^{*}}^{\mathcal{Q}}
$$
Bond prices are given by $D(t, T)=\exp \left(A(t, T)+B_{x_{1}}(t, T) x_{1, t}\right)$, where, in general, $B_{x}(t, T) \equiv \frac{1-e^{-x t}}{x}$ and
$$
A(t, T) \equiv-\delta \tau+\frac{1}{2} \frac{\sigma_{1}^{2}}{x_{1}^{2}}\left[\tau-2 B_{x_{1}}(t, T)+B_{2 x_{1}}(t, T)\right]
$$