Tag Archives: STAT0025代考

优化算法|STAT0025 Optimisation Algorithms代写

0
Posted on by

This module aims to provide an introduction to the ideas underlying the optimal choice of component variables, possibly subject to constraints, that maximise (or minimise) an objective function. The algorithms described are both mathematically interesting and applicable to a wide variety of complex real-life situations.

这是一份UCL伦敦大学学院STAT0025作业代写的成功案

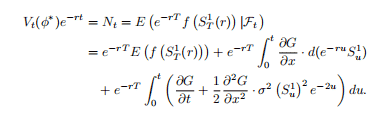
优化算法|STAT0025 Optimisation Algorithms代写
问题 1.

there is a flow of diffeomorphisms $x \rightarrow \xi_{s, t}(x)$ associated with this system, together with their non-singular Jacobians $D_{s, t}$.

In the terminology of Harrison and Pliska [150], the return process $Y_{t}=\left(Y_{t}^{1}, \ldots, Y_{t}^{d}\right)$ is here given by
$$
d Y_{t}=(\mu-\rho) d t+\Lambda d W_{t}
$$

证明 .

can be removed by applying the Girsanov change of measure. Write
$$
\eta(t, S)=\Lambda(t, S)^{-1}(\mu(t, S)-\rho),
$$
and define the martingale $M$ by
$$
M_{t}=1-\int_{0}^{t} M_{s} \eta\left(s, S_{s}\right)^{\prime} d W_{s}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

STAT0025 COURSE NOTES ：

Consider a standard Brownian motion $\left(B_{t}\right){t \geq 0}$ defined on $(\Omega, \mathcal{F}, P)$. The filtration $\left(\mathcal{F}{t}\right)$ is that generated by $B$. Recall that $B_{t}$ is normally distributed, and
$$
P\left(B_{t}<x\right)=\Phi\left(\frac{x}{\sqrt{t}}\right)
$$
Therefore
$$
P\left(B_{t} \geq x\right)=1-\Phi\left(\frac{x}{\sqrt{t}}\right)=\Phi\left(-\frac{x}{\sqrt{t}}\right)
$$
For a real-valued process $X$, we shall write
$$
M_{t}^{X}=\max {0 \leq s \leq t} X{s}, \quad m_{t}^{X}=\min {0 \leq s \leq t} X{s}
$$


运营研究中的优化算法|Optimisation Algorithms in Operational Research代写STAT0025代考

0
Posted on by

这是一份UCL伦敦大学学院STAT0025作业代写的成功案

运营研究中的优化算法|Optimisation Algorithms in Operational Research代写STAT0025代考
问题 1.

$$
z^{\prime}=15\left(\frac{51}{23}\right)-5\left(\frac{58}{23}\right)+10\left(\frac{9}{23}\right)=\frac{565}{23} \text {. }
$$
We see from Tableau $3.18$ that an optimal solution to the primal problem is
$$
x_{1}=\frac{120}{23}, \quad x_{2}=\frac{65}{23}, \quad x_{3}=\frac{15}{23}
$$
and the value of the objective function is $\frac{565}{23}$, which is the same as the value for the dual problem.

We can also solve the primal problem using the big $M$ method, obtaining the final tableau (Tableau 3.20). Using (2) we can obtain an optimal solution to the dual problem from Tableau $3.20$ as follows. Since the first initial basic variable is $x_{4}$, we then find
$$
w_{1}=\hat{w}{1}=c{4}+\left(z_{4}-c_{4}\right)=0+\frac{51}{23}=\frac{51}{23} .
$$

证明 .

The second initial basic variable is $y_{1}$, so that
$$
\hat{w}{2}=-M+\left(M-\frac{58}{23}\right)=-\frac{58}{23} . $$ But since the second constraint was multiplied by $-1$ in forming the dual problem, we must multiply $\hat{w}{2}$ by $-1$ to obtain the value of the dual variable at the optimum. We have
$$
w_{2}=-\hat{w}{2}=\frac{58}{23} \text {. } $$ Proceeding as in the case of the first dual variable, we find $$ w{3}=\hat{w}_{3}=-M+M+\frac{9}{23}=\frac{9}{23} .
$$
Substituting these values into the objective function, we get
$$
z^{\prime}=15\left(\frac{51}{23}\right)-5\left(\frac{58}{23}\right)+90\left(\frac{9}{23}\right)=\frac{565}{23}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

STAT0025 COURSE NOTES ：

  1. Maximize $z=2 x_{1}+x_{2}+3 x_{3}$ subject to
    $$
    \begin{gathered}
    2 x_{1}-x_{2}+3 x_{3} \leq 6 \
    x_{1}+3 x_{2}+5 x_{3} \leq 10 \
    2 x_{1} \quad+x_{3} \leq 7 \
    x_{1} \geq 0, \quad x_{2} \geq 0, \quad x_{3} \geq 0
    \end{gathered}
    $$
  2. Maximize $z=x_{1}+x_{2}+x_{3}+x_{4}$ subject to
    $$
    \begin{gathered}
    x_{1}+2 x_{2}-x_{3}+3 x_{4} \leq 12 \
    x_{1}+3 x_{2}+x_{3}+2 x_{4} \leq 8 \
    2 x_{1}-3 x_{2}-x_{3}+2 x_{4} \leq 7 \
    x_{1} \geq 0, \quad x_{2} \geq 0, \quad x_{3} \geq 0, \quad x_{4} \geq 0 .
    \end{gathered}
    $$