Tag Archives: umass代写

数论|Theory of Numbers代写 MATH 471

0
Posted on by

这是一份umass麻省大学 MATH 471作业代写的成功案例

数论|Theory of Numbers代写 MATH 471
问题 1.

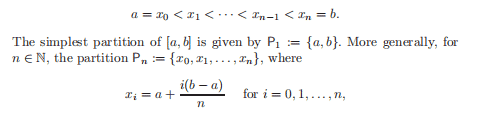
Hence
$$
L(r f)=r L(f)=r U(f)=U(r f) .
$$
On the other hand, if $r<0$, then for any partition $P$ of $[a, b]$, we see that
$$
L(P, r f)=r U(P, f) \quad \text { and } \quad U(P, r f)=r L(P, f)
$$

证明 .

and so
$$
L(r f)=r U(f)=r L(f)=U(r f) .
$$
In both the cases, we see that $r f$ is integrable and
$$
\int_{a}^{b}(r f)(x) d x=r \int_{a}^{b} f(x) d x .
$$


英国论文代写Viking Essay为您提供作业代写代考服务

MMATH 471 COURSE NOTES ：

Hence
$$
F(x)-F(a)=\sum_{i=1}^{n}\left[F\left(x_{i}\right)-F\left(x_{i-1}\right)\right]=\sum_{i=1}^{n} g\left(s_{i}\right)\left(x_{i}-x_{i-1}\right)
$$
and so
$$
L\left(P_{e}, g\right) \leq F(x)-F(a) \leq U\left(P_{e}, g\right)
$$
Since we also have
$$
L\left(P_{\epsilon}, g\right) \leq \int_{a}^{x} g(t) d t \leq U\left(P_{\epsilon}, g\right)
$$





数学建模|Mathematical Modeling代写 MATH 456

0
Posted on by

这是一份umass麻省大学 MATH 456作业代写的成功案例

数学建模|Mathematical Modeling代写 MATH 456
问题 1.

As for $n=n_{t}(a, t)$, we see that
$$
\left(a^{\prime}-a\right) \wedge\left(a^{\prime \prime}-a\right)=e^{\prime} \wedge e^{\prime \prime}\left(=O\left(\lambda^{2}\right)\right)=n_{0} \delta \Gamma_{0}+O\left(\lambda^{3}\right),
$$
where $n_{0}=n_{0}(a, t)$ and $\delta \Gamma_{0}=\delta \Gamma_{0}(a, t)$ is the area of the parallelepiped constructed over $e^{\prime}$ and $e^{\prime \prime}$; hence
$$
n_{i} \frac{\partial \Phi_{i}}{\partial a_{\alpha}} \delta \Gamma_{t}=n_{0 \alpha} \operatorname{det} \mathbf{F} \delta \Gamma_{0}+O\left(\lambda^{3}\right),
$$

证明 .

and, in vector form,
$$
n_{0} \operatorname{det} \mathbf{F} \delta \Gamma_{0}=\mathbf{F}^{T} \cdot n_{t} \delta \Gamma_{t}+O\left(\lambda^{3}\right) .
$$
Since $n_{0}$ has norm 1 , this also gives
$$
(\operatorname{det} \mathbf{F})^{2}\left(\delta \Gamma_{0}\right)^{2}=n_{t}^{T} \cdot \mathbf{F} \cdot \mathbf{F}^{T} \cdot n_{t}\left(\delta \Gamma_{t}\right)^{2}+O\left(\lambda^{5}\right),
$$
or, since $B=\mathbf{F} \cdot \mathbf{F}^{T}$ (see Section 5.1),
$$
(\operatorname{det} \mathbf{F})^{2}\left(\delta \Gamma_{0}\right)^{2}=n_{t}^{T} \cdot B \cdot n_{t}\left(\delta \Gamma_{t}\right)^{2}+O\left(\lambda^{5}\right) .
$$


英国论文代写Viking Essay为您提供作业代写代考服务

MMATH 456 COURSE NOTES ：

If we know that
$$
\frac{d}{d t} \int_{\Omega_{t}^{\prime}} C d x=\int_{\Omega_{t}^{\prime}} f d x, \quad \forall \Omega_{t}^{\prime} \subset \Omega_{t}
$$
then
$$
\frac{\partial C}{\partial t}+\operatorname{div}(C U)=f \quad \text { in } \Omega_{t}^{i}, \quad i=1,2,
$$
and
$$
\int_{\Sigma_{i}^{\prime}}[C V] \cdot N d \Gamma=0, \quad \forall \Sigma_{t}^{\prime} \subset \Sigma_{t} ;
$$
hence,
$$
[C V] \cdot N=0 \text { on } \Sigma_{t} .
$$
When $C$ is a scalar, setting $v=V \cdot N$, we rewrite the last relation as
$$
(C v){2}-(C v){1}=0 .
$$





精算金融数学|Actuarial Financial Math代写 MATH 437

0
Posted on by

这是一份umass麻省大学 MATH 437作业代写的成功案例

精算金融数学|Actuarial Financial Math代写 MATH 437
问题 1.

To see this, note that the increments of $M_{t}$ over small intervals $\Delta$ will be given by
$$
\Delta M_{t}=\Delta N_{t}^{C}-\Delta N_{t}^{B}
$$
Apply the conditional expectation operator:
$$
E_{l}\left[\Delta M_{t}\right]=E_{t}\left[\Delta N_{t}^{G}\right]-E_{t}\left[\Delta N_{f}^{B}\right]
$$

证明 .

But, approximately,
$$
\begin{aligned}
E_{f}\left[\Delta N_{t}^{G}\right] & \cong 0 \cdot(1-\lambda \Delta)+1 \cdot \lambda \Delta \
& \cong \lambda \Delta
\end{aligned}
$$
and similarly for $E_{t}\left[\Delta N_{t}^{B}\right]$. This means that
$$
E_{t}\left[\Delta M_{i}\right] \cong \lambda \Delta-\lambda \Delta=0 .
$$


英国论文代写Viking Essay为您提供作业代写代考服务

MMATH 437 COURSE NOTES ：

The discrete equivalent of the martingale representation in is then given by the following equation:
$$
C_{T}=C_{t}+\sum_{i=1}^{n} D_{t_{i}} \Delta+\sum_{i=1}^{n} g\left(C_{t_{t}}\right) \Delta M_{t_{i}}
$$
where $\Delta M_{t_{\mathrm{r}}}$ means
$$
\Delta M_{t_{1}}=M_{t_{i-1}}-M_{t_{j}}
$$
and $n$ is such that
$$
t_{v}=t<\ldots<t_{n}=T .
$$




复杂变量|Complex Variables代写 MATH 421

0
Posted on by

这是一份umass麻省大学 MATH 421作业代写的成功案例

复杂变量|Complex Variables代写 MATH 421
问题 1.

PROOF. We suppose that the series of absolute terms
$$
S=\sum_{n=1}^{\infty}\left|z_{n}\right|=\sum_{n=1}^{\infty} \sqrt{x_{n}^{2}+y_{n}^{2}}
$$
is convergent. Hence, it follows from the inequalities
$$
\left|x_{n}\right| \leq \sqrt{x_{n}^{2}+y_{n}^{2}}, \quad\left|y_{n}\right| \leq \sqrt{x_{n}^{2}+y_{n}^{2}}
$$

证明 .

and the comparison test for series of positive numbers that the series
$$
\sum_{n=1}^{\infty}\left|x_{n}\right|, \quad \sum_{n=1}^{\infty}\left|y_{n}\right|
$$
converge. Therefore, by Theorem 4.1.6, the two series
$$
S_{x}=\sum_{n=1}^{\infty} x_{n}, \quad S_{y}=\sum_{n=1}^{\infty} y_{n}
$$
also converge, that is, the series
$$
\sum_{n=1}^{\infty} z_{n}=\sum_{n=1}^{\infty}\left(x_{n}+i y_{n}\right)=S_{x}+i S_{y}
$$


英国论文代写Viking Essay为您提供作业代写代考服务

MMATH 421 COURSE NOTES ：

On the other hand, the series
$$
\sum_{n=1}^{\infty}(-1)^{n} \frac{2+3 i}{n}
$$
is only conditionally convergent since the series of absolute terms
$$
\sum_{n=1}^{\infty}\left|\frac{2+3 i}{n}\right|
$$
diverges.
As in the real case, the converse of Theorem 4.1.7 is not true in general. For instance, the series
$$
\sum_{n=1}^{\infty}(-1)^{n} \frac{2+3 i}{n}
$$
is convergent (its real and imaginary parts are conditionally convergent series), but the series
$$
\sum_{n=1}^{\infty} \frac{|2+3 i|}{n}=\sqrt{13} \sum_{n=1}^{\infty} \frac{1}{n}
$$
is divergent.




抽象代数入门I|Introduction to Abstract Algebra I代写 MATH 411

0
Posted on by

这是一份umass麻省大学 MATH 411作业代写的成功案例

抽象代数入门I|Introduction to Abstract Algebra I代写 MATH 411
问题 1.

Proof. If every $A_{n}$ is injective, or if every $C_{n}$ is projective, then the sequence $0 \longrightarrow A_{n} \longrightarrow B_{n} \longrightarrow C_{n} \longrightarrow 0$ splits; hence the sequence
$$
0 \longrightarrow \operatorname{Hom}{R}\left(C{n}, G\right) \longrightarrow \operatorname{Hom}{R}\left(B{n}, G\right) \longrightarrow \operatorname{Hom}{R}\left(A{n}, G\right) \longrightarrow 0
$$

证明 .

splits, in particular is short exact; then
$$
0 \longrightarrow \operatorname{Hom}{R}(\mathcal{C}, G) \longrightarrow \operatorname{Hom}{R}(\mathcal{B}, G) \longrightarrow \operatorname{Hom}_{R}(\mathcal{A}, G) \longrightarrow 0
$$
is a short exact sequence of complexes (of abelian groups), which is natural in $\varepsilon$ and $G$, and the result follows.


英国论文代写Viking Essay为您提供作业代写代考服务

MMATH 411 COURSE NOTES ：

applied to $\alpha, \beta, \gamma$, yields an exact sequence
$$
\operatorname{Hom}{R}(A, J) \longrightarrow \operatorname{Hom}{R}(A, L) \longrightarrow \mathrm{LExt}{R}^{1}(A, B) \longrightarrow 0 . $$ So does the first row of the diagram: $$ \operatorname{Hom}{R}(A, J) \longrightarrow \operatorname{Hom}{R}(A, L) \longrightarrow \operatorname{RExt}{R}^{1}(A, B) \longrightarrow 0 .
$$




数学计算|Mathematical Computing代写 MATH 397C

0
Posted on by

这是一份umass麻省大学 MATH 397C作业代写的成功案例

数学计算|Mathematical Computing代写 MATH 397C
问题 1.

A quantum circuit which models the phase-flip channel is shown in Fig. 6. Let $\rho_{S}$ be the first qubit input state while $(1-p)|0\rangle\langle 0|+p| 1\rangle\langle 1|$ be the second qubit input state. The circuit is the inverted controlled $-\sigma_{z}$ gate
$$
V=I \otimes|0\rangle\left\langle 0\left|+\sigma_{z} \otimes\right| 1\right\rangle\langle 1| .
$$
The output of this circuit is
$$
\begin{aligned}
&V\left(\rho_{S} \otimes[(1-p)|0\rangle\langle 0|+p| 1\rangle\langle 1|]\right) V^{\dagger} \
&=(1-p) \rho_{S} \otimes|0\rangle\left\langle 0\left|+p \sigma_{z} \rho_{S} \sigma_{z} \otimes\right| 1\right\rangle\langle 1|
\end{aligned}
$$

证明 .

from which we obtain
$$
\mathcal{E}\left(\rho_{S}\right)=(1-p) \rho_{S}+p \sigma_{z} \rho_{S} \sigma_{z}
$$
The second qubit input state may be a pure state
$$
\left|\psi_{E}\right\rangle=\sqrt{1-p}|0\rangle+\sqrt{p}|1\rangle,
$$
for example. Then we find
$$
\mathcal{E}\left(\rho_{S}\right)=\operatorname{tr}{E}\left[V \rho{S} \otimes\left|\psi_{E}\right\rangle\left\langle\psi_{E}\right| V^{\dagger}\right]=E_{0} \rho_{S} E_{0}^{\dagger}+E_{1} \rho_{S} E_{1}^{\dagger}
$$
where the Kraus operators are
$$
E_{0}=\left\langle 0|V| \psi_{E}\right\rangle=\sqrt{1-p} I, E_{1}=\left\langle 1|V| \psi_{E}\right\rangle=\sqrt{p} \sigma_{z}
$$


英国论文代写Viking Essay为您提供作业代写代考服务

MMATH 397C COURSE NOTES ：

(1) For any $a, b, c \in G$ we have
$$
\mu(a, \mu(b, c))=\mu(\mu(a, b), c) .
$$
(2) For any $a \in G$ there exists an element $e \in G$ such that
$$
\mu(a, e)=\mu(e, a)=a,
$$
where $e$ is called a unit element of $G$.
(3) For any $a \in G$ there exists an element $a^{\prime} \in G$ such that
$$
\mu\left(a, a^{\prime}\right)=\mu\left(a^{\prime}, a\right)=e,
$$
where $a^{\prime}$ is called an inverse element of $a$ and we write $a^{-1} \in G$.




数学写作|Writing in Mathematics代写 MATH 307

0
Posted on by

这是一份umass麻省大学 MATH 307作业代写的成功案例

数学写作|Writing in Mathematics代写 MATH 307
问题 1.

We return to the formulation of the Rjemann Hypothesis given in $\S 3$ above. We consider the differential operator
$$
\left(\frac{1}{2 \pi} \frac{d^{2}}{d X^{2}}+X \frac{d}{d X}+\frac{1}{2}\right)
$$
and its formal adjoint

证明 .

$$
\left(\frac{1}{2 \pi} \frac{d^{2}}{d X^{2}}-X \frac{d}{d X}+\frac{1}{2}\right)
$$

英国论文代写Viking Essay为您提供作业代写代考服务

MATH 307 COURSE NOTES ：

$$
(f, g){0}=\sum{n=1}^{\infty}\left(f, \phi_{n}^{}\right) \overline{\left(g, \phi_{n}\right)} . $$ For $f \in \hat{H}{B^{2}}$, there is an eigen-function expansion $$ f=\sum{n}\left(f, \phi_{n}^{}\right) \phi_{n}
$$
and so the definition is consistent with Parseval’s formula when that is applicable. In particular, we have
$$
|\gamma|_{0}=\sum_{n=1}^{\infty}\left(\gamma, \phi_{n}^{*}\right) \overline{\left(\gamma, \phi_{n}\right)}
$$




数学的基本概念|Fundamental Concepts of Mathematics代写 MATH 300

0
Posted on by

这是一份umass麻省大学 MATH 300作业代写的成功案例

数学的基本概念|Fundamental Concepts of Mathematics代写 MATH 300
问题 1.

Proof. Recall the notation for continued fractions. Since $\alpha$ is a quadratic irrational, there exists a minimal integer $p$, called the period of $\alpha$, such that $\alpha=\left[a_{1}, a_{2}, \ldots, a_{p}, a_{1}, a_{2}, \ldots, a_{p}, a_{1}\right.$, $\left.a_{2}, \ldots, a_{p}, \ldots\right]$. That is, $a_{k+i}=a_{i}$ if $k$ is a multiple of $p$.
Hence,
$$
q_{k+i}=a_{i} q_{k-1+i}+q_{k-2+i}, \quad 0 \leq i \leq p
$$

证明 .

We estimate the difference of the last two series. Observe that
$$
\sum_{i=q_{k}+1}^{q_{n+k}} \chi_{I_{U}}\langle i \alpha\rangle=\sum_{i=q_{j}+1}^{q_{n+j}} \chi_{I_{V}}\langle i \alpha\rangle .
$$

英国论文代写Viking Essay为您提供作业代写代考服务

MATH 300 COURSE NOTES ：

The entropy of $\Gamma$ verifies the inequality
$$
S(\Gamma) \leq S_{t}(\Gamma):=\log \frac{2|\Gamma|}{|\partial K|}+\frac{\beta}{e^{\beta}-1}
$$
where
$$
\beta=\log \frac{2|\Gamma|}{2|\Gamma|-|\partial K|}>0
$$
Proof: Maximize the function
$$
S\left(p_{1}, p_{2}, \ldots\right)=\sum_{n=1}^{\infty} p_{n} \log \frac{1}{p_{n}}
$$




代数、解析几何和三角学|Algebra, Analytic Geometry and Trigonometry代写 MATH 104

0
Posted on by

这是一份umass麻省大学 MATH 103作业代写的成功案例

代数、解析几何和三角学|Algebra, Analytic Geometry and Trigonometry代写 MATH 104
问题 1.

$\operatorname{proj}{o x} O P=\operatorname{proj}{o x} O A+\operatorname{proj}_{o x} A P .$
By the first projection theorem, this becomes:
$$
O P \cos (\alpha+\beta)=O A \cos \alpha+A P \cos \left(90^{\circ}+\alpha\right) .
$$
Or, since
$$
\cos \left(90^{\circ}+\alpha\right)=-\sin \alpha,
$$

证明 .

we have:
$O P \cos (\alpha+\beta)=O A \cos \alpha-A P \sin \alpha$
Dividing by $O P$, we have:
$$
\cos (\alpha+\beta)=\cos \alpha\left(\frac{O A}{O P}\right)-\sin \alpha\left(\frac{A P}{O P}\right)
$$
Or, since
$$
\frac{O A}{O P}=\cos \beta
$$
and
$$
\frac{A P}{O P}=\sin \beta
$$

英国论文代写Viking Essay为您提供作业代写代考服务

MATH104 COURSE NOTES ：

Hence we have:
$$
\cos \alpha=1-2 \sin ^{2} \frac{\alpha}{2}
$$
or:
$$
2 \sin ^{2} \frac{\alpha}{2}=1-\cos \alpha
$$
or:
$$
\sin ^{2} \frac{\alpha}{2}=\frac{1-\cos \alpha}{2} .
$$
Or, finally,
$$
\sin \frac{\alpha}{2}=\pm \sqrt{\frac{1-\cos \alpha}{2}}
$$




预微积分和三角学|Precalculus and Trigonometry代写 MATH 103

0
Posted on by

这是一份umass麻省大学 MATH 103作业代写的成功案例

预微积分和三角学|Precalculus and Trigonometry代写 MATH 103
问题 1.

Proof
Drop a perpendicular $h$ from $C$ to $A B$ at $M$.
Then
and
$$
\begin{aligned}
&h^{2}=b^{2}-\overline{A M}^{2}, \
&h^{2}=a^{2}-\overline{M B}^{2} .
\end{aligned}
$$

证明 .

Equating, we have:
$$
a^{2}-\overline{M B}^{2}=b^{2}-\overline{A M}^{2},
$$
or:
$$
a^{2}=b^{2}+\overline{M B}^{2}-\overline{A M}^{2}
$$
Then, since
and
$$
\begin{aligned}
&M B=c-A M \
&=c^{2}-2 c(A M)+\overline{A M}^{2},
\end{aligned}
$$

英国论文代写Viking Essay为您提供作业代写代考服务

MATH103 COURSE NOTES ：

Solve the triangle; given $a=20.63, b=34.21, c=40.17$.
We have:
$$
\cos A=\frac{b^{2}+c^{2}-a^{2}}{2 b c} .
$$
By the table of squares,
$$
\begin{aligned}
&a^{2}=425.6 \
&b^{2}=1171 \
&c^{2}=1614
\end{aligned}
$$
(The interpolation is exactly the same as in logarithms.)