Tag Archives: 代数几何学代写

代数几何学 Algebraic Geometry MATH0076

0
Posted on by

这是一份UCL伦敦大学 MATH0076作业代写的成功案例

代数几何学 Algebraic Geometry MATH0076
问题 1.


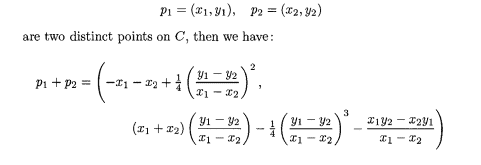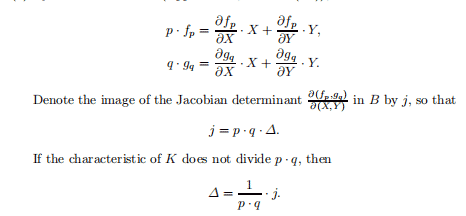
$$
\operatorname{dim}{K} \frac{\overline{\mathcal{O}}{F, P}}{\mathcal{O}{F, P}}+\operatorname{dim}{K} \frac{\mathcal{O}{F, P}}{(\gamma)}=\operatorname{dim}{K} \frac{\overline{\mathcal{O}}{F, P}}{(\gamma)}+\operatorname{dim}{K} \frac{\gamma \overline{\mathcal{O}}{F, P}}{\gamma \mathcal{O}{F, P}} .
$$
Since $\gamma$ is not a zero divisor of $\overline{\mathcal{O}}{F, P}$, the $K$-vector spaces $\overline{\mathcal{O}}{F, P} / \mathcal{O}{F, P}$ and $\gamma \overline{\mathcal{O}}{F, P} / \gamma \mathcal{O}_{F, P}$ are isomorphic, and so


证明 .

$$
\mu_{P}(F, G)=\operatorname{dim}{K} \overline{\mathcal{O}}{F, P} /(\gamma) .
$$
As in the proof of we have
$$
\overline{\mathcal{O}}{F, P} /(\gamma) \cong R{1} /(\gamma) \times \cdots \times R_{h} /(\gamma)
$$
and then from E.13,
$$
\operatorname{dim}{K} \overline{\mathcal{O}}{F, P} /(\gamma)=\sum_{i=1}^{h} \operatorname{dim}{K}\left(R{i} /(\gamma)\right)=\sum_{i=1}^{h} \nu_{R_{i}}(\gamma)
$$

英国论文代写Viking Essay为您提供作业代写代考服务

MATH0076 COURSE NOTES ：



$$
\varepsilon: S\left[X_{1}, X_{2}\right] \rightarrow A[X, Y] \quad\left(X_{1} \mapsto X, X_{2} \mapsto Y\right)
$$
and
$$
\delta: S\left[X_{1}, X_{2}\right] \rightarrow B[X, Y] \quad\left(X_{1} \mapsto X, X_{2} \mapsto Y\right) .
$$
Here $\varepsilon(F)=f, \varepsilon(G)=g, \delta(F)=G f, \delta(G)=G g$, so that by $\varepsilon$ the induced epimorphism
$$
S\left[X_{1}, X_{2}\right] /(F, G) \rightarrow A[X, Y] /(f, g)
$$
can be identified with the canonical epimorphism $S^{e} \rightarrow A^{e}$ and
$$
S\left[X_{1}, X_{2}\right] /(F, G) \rightarrow B[X, Y] /(G f, G g)
$$
with $S^{e} \rightarrow B^{e}$.






代数几何学|Algebraic Geometry代写  7CCMMS20

0
Posted on by

这是一份kcl伦敦大学学院  7CCMMS20作业代写的成功案

代数几何学|Algebraic Geometry代写  7CCMMS20
问题 1.

Let $R=K\left[T_{0}, \ldots, T_{n}\right]$. Then, for $k \geq 0$
$$
\operatorname{dim} R_{k}=\text { number of monomials of degree } k \text { in } T_{0}, \ldots, T_{n}=\left(\begin{array}{c}
k+n \
n
\end{array}\right)
$$


证明 .

Hence $P_{\mathrm{p} n}=\frac{1}{n !}(T+n) \cdots \ldots \cdot(T+1)=\frac{T^{n}}{n !}+\ldots$
If $X \subset p^{n}$ is a hypersurface given by a homogeneous polynomial $F$ of degree $d$ then, for $k \geq d$,
$$
\operatorname{dim}\left(K\left[T_{0}, \ldots, T_{n}\right] /(F)\right){k}=\left(\begin{array}{c} k+n \ n \end{array}\right)-\left(\begin{array}{c} k+n-d \ n \end{array}\right) $$ whence $P{X}=\frac{d}{(n-1) !} T^{n-1}+\ldots .$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

7CCMMS20 COURSE NOTES ：

Suppose, for simplicity, that $X$ is a smooth $n$-dimensional variety, and let $Y$ and $Z$ be two subvarieties of $X$. As was shown in Chap. $2, \S 6$, we have
$$
\operatorname{dim}(Y \cap Z) \geq \operatorname{dim} Y+\operatorname{dim} Z-n
$$
If equality holds, that is, if the varieties $Y$ and $Z$ meet properly then, to each component $W$ of $Y \cap Z$, intersection theory assigns some multiplicity $i(W ; Y, Z)$, and defines the intersection of $Y$ and $Z$ to be the cycle
$$
Y \cdot Z=\sum_{W} i(W ; Y, Z) \cdot[W]
$$