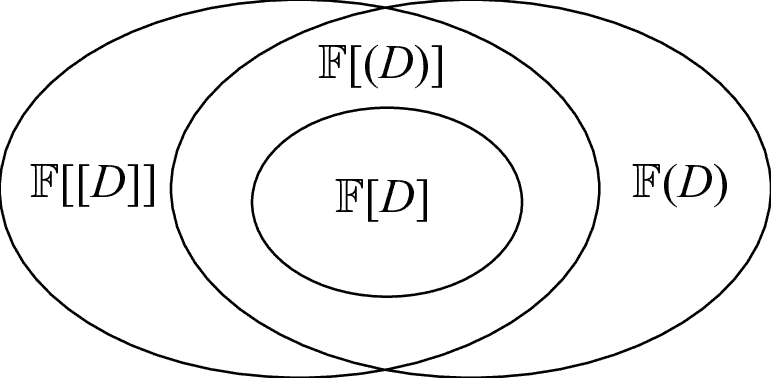
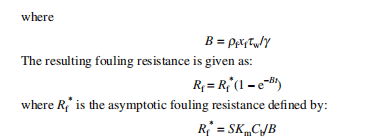By uniqueness for the initial value problem and the Intermediate Value Theorem, we have that $x(t)>0$ for all $t \in\left[0, t_{f}\right]$. It follows that $\sigma\left(t_{f}\right)>0$. If $r \geq 1$, then $\sigma \leq 0$, so that $\sigma$ is non-increasing, which combined with $\sigma\left(t_{f}\right)>0$ shows that $\sigma>0$ on $\left[0, t_{f}\right]$. We conclude that $u^{*} \equiv 0$ in that case. If $r \in(0,1)$, then $\dot{\sigma}>0$, so that $\sigma$ is strictly increasing. It follows that singular control is not possible and that there can be at most one switch.r.
这是一份Bath巴斯大学学院MA30061/MA50061作业代写的成功案
This problem fits into the standard form of the optimal control problem with
$$
\begin{gathered}
n=2, m=1, \quad h(\tau, \xi, v)=\left[\begin{array}{c}
\xi_{2} \
v
\end{array}\right], \quad f(\tau, \xi, v)=\frac{E(\tau) I(\tau)}{2} v^{2}-q(\tau) \xi_{1}, \quad \phi(\tau, \xi)=0, \
t_{0}=a, \quad t_{f}=b, \quad x_{0}=\left[\begin{array}{l}
0 \
0
\end{array}\right], \quad x\left(t_{f}\right)=\text { free, } \quad \mathscr{H}=\mathbb{R} .
\end{gathered}
$$
(2b) The Hamiltonian function is
$$
\mathcal{H}(\tau, \xi, v, \rho)=\frac{E(\tau) I(\tau)}{2} v^{2}-q(\tau) \xi_{1}+\rho_{1} \xi_{2}+\rho_{2} v
$$
We have
$$
\frac{\partial \mathcal{H}}{\partial v}=E(\tau) I(\tau) v+\rho_{2}
$$
From this we see that $v \mapsto \mathcal{H}(\tau, \xi, v, \rho)$ is minimized when
$$
E(\tau) I(\tau) v+\rho_{2}=0
$$
Therefore
$$
u^{*}(t)=\frac{-1}{E(t) I(t)} p_{2}(t)
$$
We also see that
$$
\frac{\partial \mathcal{H}^{T}}{\partial \xi}=\left[\begin{array}{c}
-q(\tau) \
\rho_{1}
\end{array}\right], \quad \frac{\partial \phi^{T}}{\partial \xi}=0
$$
The adjoint equation with transversality condition then is
$$
\dot{p}=\left[\begin{array}{c}
q \
-p_{1}
\end{array}\right], \quad p\left(t_{f}\right)=0
$$

MA30061/MA50061 COURSE NOTES :
Integrating twice gives
$$
y(t)=\frac{t^{5}}{40}+A \frac{t^{4}}{12}+B \frac{t^{3}}{6}+C t+D
$$
where $C, D \in \mathbb{R}$ are constants. The boundary conditions are
$$
y(0)=0, \quad \dot{y}(0)=0, \quad \ddot{y}(1)=0, \quad\left(\frac{d}{d t} \frac{1}{t} \ddot{y}(t)\right)(1)=0 .
$$
The first of these gives $D=0$ whereas the second gives $C=0$. From the third we obtain
$$
\frac{1}{2}+A+B=0
$$
whereas from the fourth we obtain
$$
1+A=0
$$
Hence we obtain $A=-1$ and $B=\frac{1}{2}$. Therefore
$$
y(t)=\frac{t^{5}}{40}-\frac{t^{4}}{12}+\frac{t^{3}}{12}
$$