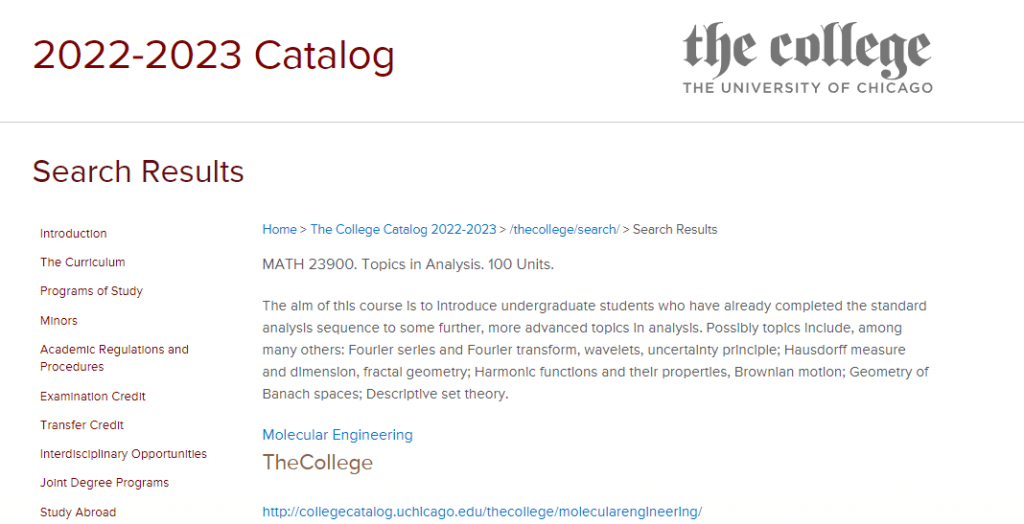
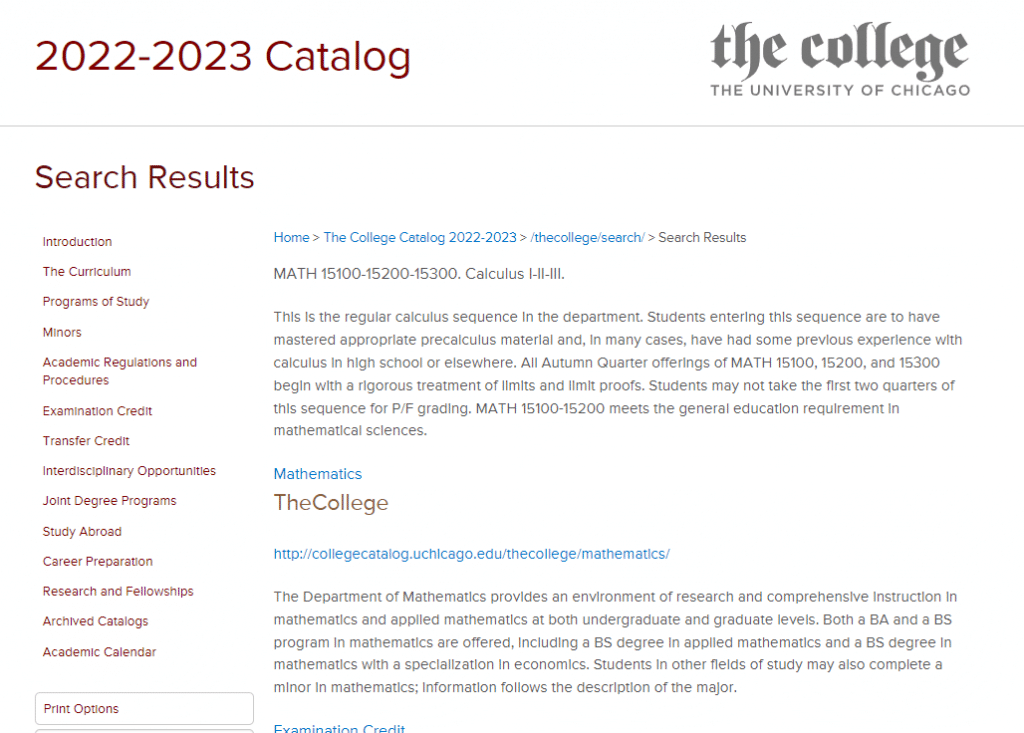
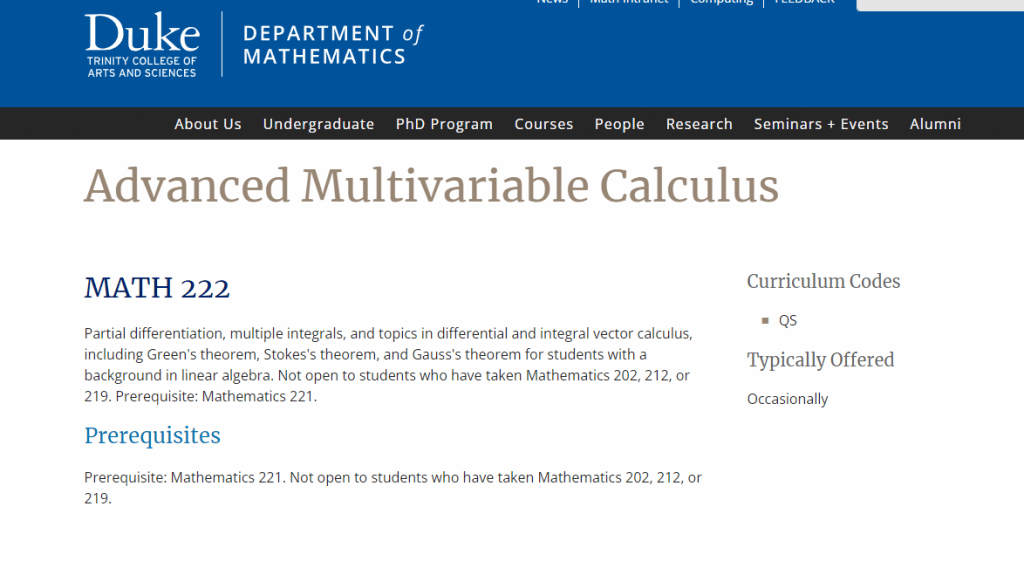
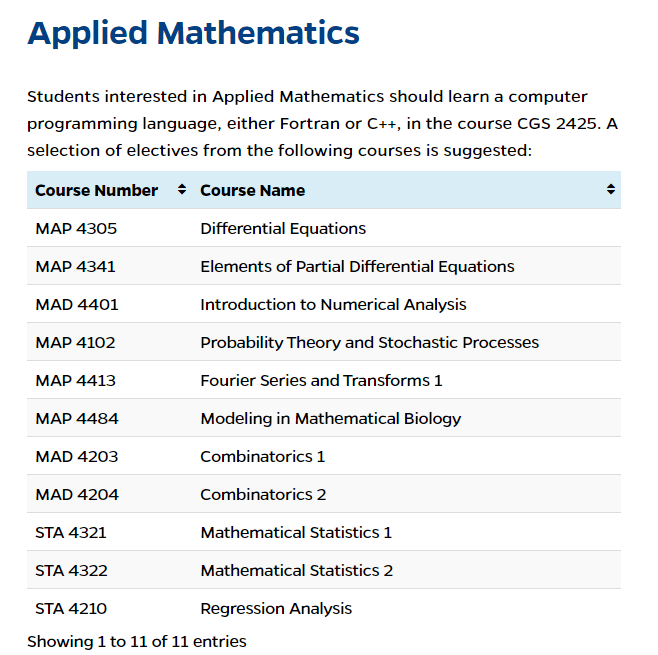
Assignment-daixieTM为您提供华盛顿大学University of WashingtonMATH 124 Calculus With Analytic Geometry I微积分与解析几何代写代考和辅导服务!
Instructions:
If you are searched for the ebook Calculus with analytic geometry student solution manual in pdf form, then you have come on to loyal website. We present full version of this book in ePub, txt, doc, DjVu, PDF forms. You can read online Calculus with analytic geometry student solution manual or load. As well, on our website you can read guides and other art books online, or load them. We will to draw on your attention that our site does not store the book itself, but we grant link to website whereat you may load either reading online. So that if have must to downloading pdf Calculus with analytic geometry student solution manual, then you have come on to faithful website. We have Calculus with analytic geometry student solution manual PDF, DjVu, ePub, txt, doc forms. We will be happy if you go back to us afresh.
Let $W$ be a function which assigns to every function $F$ and any interval $[a, b]$ over which $F$ is integrable a real number $W(F, a, b)$ such that (5.1), (5.2), and (5.3) hold. Then
$$
W(F, a, b)=\int_a^b F(x) d x
$$
Proof. Let $F$ be a function, and $[a, b]$ an interval over which $F$ is integrable. We shall first show that, for every partition $\sigma$ of $[a, b]$, the upper and lower sums, $U_\sigma$ and $L_\sigma$, satisfy the inequalities
$$
L_\sigma \leq W(F, a, b) \leq U_\sigma
$$
To do this, we let $\sigma=\left{x_0, \ldots, x_n\right}$ and assume the usual ordering:
$$
a=x_0 \leq x_1 \leq \cdots \leq x_n=b .
$$
As we have done in the past, we denote by $M_i$ the least upper bound of the values of $F$ on the ith subinterval $\left[x_{i-1}, x_i\right]$, and by $m_i$ the greatest lower bound. Then
$$
m_i \leq F(x) \leq M_i, \quad \text { whenever } x_{i-1} \leq x \leq x_i
$$
The two constant functions with values Mi and mi, respectively, are certainly integrable over the subinterval $\left[x_{i-1}, x_i\right]$. Following the common practice of denoting a constant function by its value, we know, as a result of (5.2), that
$$
W\left(m_i, x_{i-1}, x_i\right) \leq W\left(F, x_{i-1}, x_i\right) \leq W\left(M_i, x_{i-1}, x_i\right)
$$
Using (5.3), we obtain
$$
\begin{aligned}
& W\left(m_i, x_{i-1}, x_i\right)=m_i\left(x_i-x_{i-1}\right) \
& W\left(M_i, x_{i-1}, x_i\right)=M_i\left(x_i-x_{i-1}\right)
\end{aligned}
$$
Hence
$$
m_i\left(x_i-x_{i-1}\right) \leq W\left(F, x_{i-1}, x_i\right) \leq M_i\left(x_i-x_{i-1}\right) .
$$
Adding these inequalities for $i=1, \ldots, n$, we get
$$
\sum_{i=1}^n m_i\left(x_i-x_{i-1}\right) \leq \sum_{i=1}^n W\left(F, x_{i-1}, x_i\right) \leq \sum_{i=1}^n M_i\left(x_i-x_{i-1}\right) .
$$
The left and right sides of the inequalities in the preceding equation are precisely $L_\sigma$ and $U_\sigma$, respectively. It follows from repeated use that
$$
\sum_{i=1}^n W\left(F, x_{i-1}, x_i\right)=W(F, a, b)
$$
and we have therefore proved that the inequalities do hold.
now essentially complete. Let $\sigma$ and $\tau$ be two arbitrary partitions of $[a, b]$. The union $U \cup T$ is the partition which is the common refinement of both. It is shown in the last line of the proof of Proposition (1.1), page 168, that
$$
L_\sigma \leq L_{\sigma \cup \tau} \leq U_{\sigma \cup \tau} \leq U_\tau
$$
If f is bounded on [a, b] and is continuous at every point of [a, b] except possibly at the endpoints, then f is integrable over [a, b].
Proof. If $a=b$, the conclusion follows at once since $\int_a^b f=\int_a^a f=0$. Hence we shall assume that $a<b$. To be specific, we shall furthermore assume that $f$ is continuous at every point of $[a, b]$ except at $a$. The necessary mod)fication in the argument if a discontinuity occurs at $b$ (or at both $a$ and $b$ ) should be obvious. According to the definition of integrability (page 168), it is sufficient to prove that there exist partitions $\sigma$ and $\tau$ of $[a, b]$ such that $U_\sigma-L_\tau$, the difference between the corresponding upper and lower sums, is arbitrarily small. For this purpose, we choose an arbitrary positive number $\epsilon$. Since $f$ is bounded on $[a, b]$, there exists a positive number $k$ such that $|f(x)| \leq k$, for every $x$ in $[a, b]$. We next pick a point $a^{\prime}$ which is in $[a, b]$ and sufficiently close to a that
$$
0<a^{\prime}-a<\frac{\epsilon}{3 k}
$$
(see Figure 26). Since $f$ is continuous on the smaller interval $\left[a^{\prime}, b\right]$, we know that $f$ is integrable over it. Hence there exist partitions $\sigma^{\prime}$ and $\tau^{\prime}$ of $\left[a^{\prime}, b\right]$ such that the upper sum $U_{\sigma^{\prime}}$, and lower sum $L_{\tau^{\prime}}$ for $f$ satisfy
$$
\left|U_{\sigma^{\prime}}-L_{\tau^{\prime}}\right|<\frac{\epsilon}{3}
$$
Let $\sigma$ and $\tau$ be the partitions of $[a, b]$ obtained from $\sigma^{\prime}$ and $\tau^{\prime}$ respectively, by adjoining the point $a$; i.e., $\sigma=\sigma^{\prime} \cup{a}$ and $\tau=\tau^{\prime} \cup{a}$. Since the maximum value of $|f(x)|$ on the subinterval $\left[a, a^{\prime}\right]$ is less than or equal to $k$, it follows that
$$
\left|U_\sigma-U_{\sigma^{\prime}}\right| \leq k\left(a^{\prime}-a\right)<k \cdot \frac{\epsilon}{3 k}=\frac{\epsilon}{3} .
$$
By the same argument, we have
$$
\left|L_{\tau^{\prime}}-L_\tau\right| \leq k\left(a^{\prime}-a\right)<k \cdot \frac{\epsilon}{3 k}=\frac{\epsilon}{3} .
$$
Next, consider the algebraic identity
$$
U_\sigma-L_\tau=\left(U_\sigma-U_{\sigma^{\prime}}\right)+\left(L_{\tau^{\prime}}-L_\tau\right)+\left(U_{\sigma^{\prime}}-L_{\tau^{\prime}}\right) .
$$
Let $[a, b]$ be a subset of the domains of two functions $f$ and $g$, and let $f(x)=$ $g(x)$ for all but afinite number of values of $x$ in $[a, b]$. If $f$ is integrable over $[a, b]$, then so is $g$ and $\int_a^b f=\int_a^b g$.
Proof. It is sufficient to prove this theorem under the assumption that the values of $f$ and $g$ differ at only a single point $c$ in the interval $[a, b]$ (because the result can then be iterated). To be specific, we shall assume that $f(c)<g(c)$. The proof is completed if we can show that there exist upper and lower sums for $g$ which differ from the integral $\int_a^b f$ by an arbitrarily small amount. For this purpose, we choose an arbitrary positive number $\epsilon$. Since $f$ is, by hypothesis, integrable over $[a, b]$, there exists a partition $\tau$ of $[a, b]$ such that the corresponding lower sum for $f$, which we denote by $L_\tau(f)$, satisfies
$$
\int_a^b f L_\tau(f)<\epsilon .
$$
However, every lower sum for $f$ is also a lower sum for $g$. Hence we may substitute $L_\tau(g)$ for $L_\tau(f)$ in the preceding inequality and obtain
$$
\int_a^b f-L_\tau(g)<\epsilon .
$$
We next derive a similar inequality involving an upper sum for $g$. The integrability of $f$ also implies the existence of a partition $\sigma^{\prime}$ of $[a, b]$ such that the corresponding upper sum for $f$ satisfies
$$
U_{\sigma^{\prime}}(f)-\int_a^b f<\frac{\epsilon}{2} .
$$
By possibly adjoining to $\sigma^{\prime}$ a point on either side of $c$, we can assure ourselves of getting a partition $\sigma=\left{x_0, \ldots, x_n\right}$ of $[a, b]$ with the property that if $c$ lies in the ith subinterval $\left[x_{i-1}, x_i\right]$, then
$$
x_i-x_{i-1}<\frac{\epsilon}{2[g(c)-f(c)]}
$$