这是一份umass麻省大学 STAT 525作业代写的成功案例
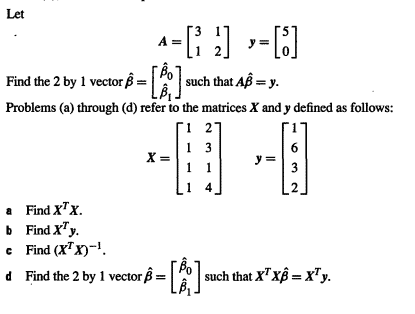
Population regression function, or simply, the regression function:
$$
\mu_{Y}(x)=\beta_{0}+\beta_{1} x \quad \text { for } a \leq x \leq b
$$
Sample regression function:
$$
\hat{\mu}{Y}(x)=\hat{\beta}{0}+\hat{\beta}{1} x $$ Population regression model, or simply, the regression model: $$ Y{I}=\beta_{0}+\beta_{1} X_{I}+E_{I} \quad \text { for } I=1, \ldots, N
$$
Sample regression model:
$$
y_{i}=\beta_{0}+\beta_{1} x_{i}+e_{i} \quad \text { for } i=1, \ldots, n
$$
A randomly chosen $Y$ value from the subpopulation determined by $X=x$ :
$$
\boldsymbol{Y}(\boldsymbol{x})
$$
Sample prediction function, or simply, prediction function:
$$
\hat{Y}(x)=\hat{\beta}{0}+\hat{\boldsymbol{\beta}}{1} \boldsymbol{x}
$$
Note: $\hat{\mu}_{Y}(x)=\hat{Y}(x)$

STAT525 COURSE NOTES :
when $X$ and $Y$ are measured using the first system of units. Also suppose the regression function is
$$
\mu_{Y^{}}\left(x^{}\right)=\beta_{0}^{}+\beta_{1}^{} x^{} $$ when $X^{}$ and $Y^{}$ are measured using the second system of units. Then it can be proved mathematically that $$ \beta_{1}^{}=\frac{d}{b} \beta_{1}
$$
and
$$
\beta_{0}^{*}=c+\frac{d}{b}\left(b \beta_{0}-a \beta_{1}\right)
$$