The course aims to introduce students to discrete mathematics, a fundamental part of mathematics with many applications in computer science and related areas. The course provides an introduction to graph theory and combinatorics, the two cornerstones of discrete mathematics. The course will be offered to third or fourth year students taking Mathematics degrees, and might also be suitable for students from other departments. There will be an emphasis on extremal results and a variety of methods.
这是一份UCL伦敦大学学院MATH0029作业代写的成功案
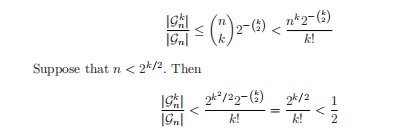

$$
(1-\epsilon) p q n=(1-\epsilon) c n \leq \sum_{i=1}^{r}\left|X_{i}\right|=r \ell \leq q \ell
$$
whence $(1-\epsilon) n \leq \epsilon \ell$ and hence $j<n \leq 2 \epsilon \ell$. Because $\left|Y_{s}\right| \geq 4^{-d_{j, k} \ell} \geq 4^{-\Delta} \ell$ and $\left(\Delta^{2}+2\right) \epsilon<4^{-\Delta}$,
$$
\left|Y_{s}\right|-\Delta^{2} \epsilon \ell-j>4^{-\Delta} \ell-\Delta^{2} \epsilon \ell-2 \epsilon \ell=\left(4^{-\Delta}-\left(\Delta^{2}+2\right) \epsilon\right) \ell>0
$$
Also, because $\epsilon<\frac{1}{4}$ and $\left|Y_{t}\right| \geq 4^{-d_{j, k} \ell}$,
$$
\left(\frac{1}{2}-\epsilon\right)\left|Y_{t}\right| \geq \frac{1}{4}\left(4^{-d_{j, k}} \ell\right)=4^{-d_{j, k}-1} \ell=4^{-d_{j+1, k} \ell}
$$

MATH0029 COURSE NOTES :
For a pair ${X, Y}$ of disjoint sets of vertices of a graph $G$, we define its index of regularity by:
$$
\rho(X, Y):=|X | Y|(d(X, Y))^{2}
$$
This index is nonnegative. We extend it to a family $\mathcal{P}$ of disjoint subsets of $V$ by setting:
$$
\rho(\mathcal{P}):=\sum_{X, Y \in \mathcal{P}} \rho(X, Y)
$$
In the case where $\mathcal{P}$ is a partition of $V$, we have:
$$
\rho(\mathcal{P})=\sum_{\substack{X \in Y \in \mathcal{P} \ X \neq Y}}|X | Y|(d(X, Y))^{2} \leq \sum_{\substack{X, Y \in \mathcal{P} \ X \neq Y}}|X||Y|<\frac{n^{2}}{2}
$$