这是一份kcl伦敦大学学院 7CCMCS03作业代写的成功案
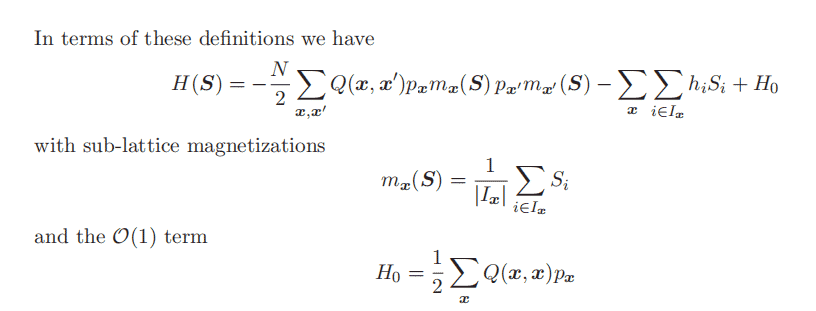
This is now explicitly of a form that can be evaluated by the saddle point method. Note also, that results do not depend on the specific realization of the randomness, but only on the distributions of the random fields $h_{i}$ and the $\boldsymbol{\xi}{i}$ ! Fixed point equations are $$ \begin{aligned} \mathrm{i} \hat{m}{\boldsymbol{x}} &=\beta \sum_{\boldsymbol{x}^{\prime}} Q\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right) p_{\boldsymbol{x}^{\prime}} m_{\boldsymbol{x}^{\prime}} \
m_{\boldsymbol{x}} &=\left\langle\tanh \left(\mathrm{i} \hat{m}{\boldsymbol{x}}+\beta h\right)\right\rangle{h}
\end{aligned}
$$
Inserting the solution of the first into the second, we get
$$
m_{\boldsymbol{x}}=\left\langle\tanh \left[\beta \sum_{\boldsymbol{x}^{\prime}} Q\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right) p_{\boldsymbol{x}^{\prime}} m_{\boldsymbol{x}^{\prime}}+\beta h\right]\right\rangle_{h},
$$

7CCMCS03COURSE NOTES :
$$
\Delta=\frac{1}{i \lambda_{\varepsilon}+J^{2} \Delta}
$$
This is a quadratic equation for $\Delta$, which is solved by
$$
\Delta_{1,2}=-\mathrm{i} \frac{\lambda_{\varepsilon}}{2 J^{2}} \pm \frac{1}{2 J^{2}} \sqrt{4 J^{2}-\lambda_{\varepsilon}^{2}}
$$
Taking the limit $\varepsilon \rightarrow 0$ we have
$$
\operatorname{Re} \Delta_{i}=\operatorname{Re} \Delta= \begin{cases}\frac{1}{2 J^{2}} \sqrt{4 J^{2}-\lambda^{2}} & ;|\lambda| \leq 2 J \ 0 & ;|\lambda|>2 J\end{cases}
$$
which when inserted into finally gives
$$
\rho(\lambda)=\frac{1}{2 \pi J^{2}} \sqrt{4 J^{2}-\lambda^{2}}, \quad|\lambda| \leq 2 J
$$