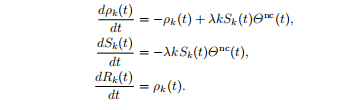
$$
S_{k}(t)=e^{-\lambda k \phi(t)}, \quad R_{k}(t)=\int_{0}^{\infty} \rho_{k}(\tau) d t
$$
where we have defined the auxiliary function
$$
\phi(t)=\int_{0}^{t} \Theta^{\mathrm{nc}}(\tau) d \tau=\frac{1}{\langle k\rangle} \sum_{k}(k-1) P(k) R_{k}(t)
$$
In order to get a closed relation for the total density of infected individuals, it results more convenient to focus on the time evolution of the averaged magnitude $\phi(t)$. To this purpose, let us compute its time derivative:
$$
\frac{d \phi(t)}{d t}=1-\frac{1}{\langle k\rangle}-\phi(t)-\frac{1}{\langle k\rangle} \sum_{k}(k-1) P(k) e^{-\lambda k \phi(t)}
$$
where we have introduced the time dependence of $S_{k}(t)$ obtained in ( $[8.37)$. Once solved (В.39]), we can obtain the total epidemic prevalence $R_{\infty}$ as a function of $\phi_{\infty}=\lim {t \rightarrow \infty} \phi(t)$. Since $R{k}(\infty)=1-S_{k}(\infty)$, we have
$$
R_{\infty}=\sum_{k} P(k)\left(1-e^{-\lambda k \phi_{\infty}}\right) .
$$

6CCMCS02 COURSE NOTES :
$$
P_{i j}^{k}(n)=\sum_{l_{1}, l_{2}, \ldots, l_{n-1}} p_{i l_{1}}^{k} p_{l_{1} l_{2}}^{k} \cdots p_{l_{n-1} j^{*}}^{k}
$$
This definition allows us to compute the average number of times, $b_{i j}^{k}$, that a packet generated at $i$ and with destination at $k$ passes through $j$.
$$
b^{k}=\sum_{n=1}^{\infty} P^{k}(n)=\sum_{n=1}^{\infty}\left(p^{k}\right)^{n}=\left(I-p^{k}\right)^{-1} p^{k}
$$
and the effective betweenness of node $j, B_{j}$, is then defined as the sum over all possible origins and destinations of the packets,
$$
B_{j}=\sum_{i, k} b_{i j}^{k}
$$