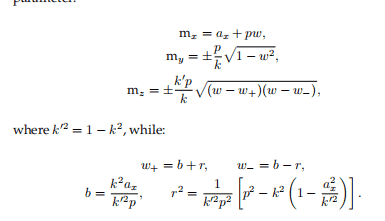这是一份liverpool利物浦大学MATH103的成功案例

Let $[., .]$ denote an indefinite inner product defined on $\mathrm{R}^{n}$ by a real symmetric invertible matrix $H$ of size $n$, i.e.,,
$$
[x, y]=(H x, y), \quad \text { for all } x, y \in \mathrm{R}^{n} .
$$
Recall that (… ) stands for the standard inner product in $\mathrm{R}^{n}$ :
$$
(x, y)=\sum_{j=1}^{n} x^{(j)} y^{(j)}
$$
where $x=\left\langle x^{(1)}, \ldots, x^{(n)}\right\rangle, y=\left\langle y^{(1)}, \ldots, y^{(n)}\right\rangle$ are vectors in $\mathrm{R}^{n}$. The adjoint $A^{[]}$ of a real $n \times n$ matrix $A$ is defined just as in (4.1.2) and, as in (4.1.3) it is easily seen that $A^{[]}=H^{-1} A^{} H$. Since $A^{}$ is now just the transpose of $A, A^{[]}$ is obviously real. The following facts and definitions are all formally identical with predecessors in earlier chapters: A real matrix $A$ is $H$-selfadjoint if $A^{}=A$, i.e., if $H A=A^{} H$. A real matrix $A$ is $H$-unitary if $A^{} A=I$, i.e., if $A^{} H A=H$. A real matrix $A$ is $H$-normal if $A^{} A=A A^{}$, i.e., if $\left(H^{-1} A^{} H\right) A=A\left(H^{-1} A^{*} H\right)$.

MATH103 COURSE NOTES ：

only if there is a $(B, G) \in S_{r}$ which can be transformed to $\left(J, P_{e, J}\right)$ by both $T_{+}$ and $T_{-}$, say, with $\operatorname{det} T_{+}>0$ and $\operatorname{det} T_{-}<0$. Thus,
$$
B=T_{+}^{-1} J T_{+}=T_{-}^{-1} J T_{-}, \quad G=T_{+}^{} P_{\varepsilon, J} T_{+}=T_{-}^{} P_{\varepsilon, J} T_{-},
$$
and it follows immediately that $U S_{+}=U S_{-}$if and only if there is a real $T$ with negative determinant such that
$$
J=T^{-1} J T, \quad P_{\varepsilon, J}=T^{*} P_{\varepsilon, J} T .
$$