Tag Archives: adelaide代写

统计机器学习|Statistical Machine Learning 代写 COMP SCI 3314 代考

0
Posted on by

这是一份adelaide阿德莱德大学 STATS 3003 作业代写的成功案

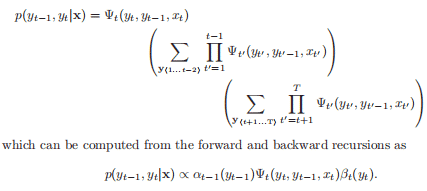
统计机器学习|Statistical Machine Learning 代写 STATS 3003 代考
问题 1.

Proof
$$
\begin{aligned}
\Phi(G) &=\prod_{g \in G} \prod_{\theta \in \Theta_{g}} \phi_{g}\left(A_{g} \theta\right)=\prod_{g \in G} \prod_{\theta \in \Theta_{G}} \phi_{g}\left(A_{g} \theta\right)^{\left|\Theta_{g}\right| /\left|\Theta_{G}\right|} \
&=\prod_{\theta \in \Theta_{G}} \prod_{g \in G} \phi_{g}\left(A_{g} \theta\right)\left|\Theta_{g}\right| /\left|\Theta_{G}\right|=\prod_{\theta \in \Theta_{G}} \phi_{f s(G)}\left(A_{G} \theta\right)=\Phi(f s(G))
\end{aligned}
$$


证明 .

While the above is correct, it is rather unnatural to have $e(D)$ and $e\left(D^{\prime}\right)$ be distinct atoms. If a set of logical variables has the same possible substitutions, like $D$ and $D^{\prime}$ here, we can do something better

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

COMP SCI 3314 COURSE NOTES ：

\begin{array}{r}
P\left(\boldsymbol{\theta}{\mathcal{G}}, \mathcal{D}\right)=P\left(\boldsymbol{\theta}{X}\right) L_{X}\left(\boldsymbol{\theta}{X}: \mathcal{D}\right) \ P\left(\boldsymbol{\theta}{Y \mid x^{1}}\right) \prod_{j: x^{j}=x^{1}} P\left(y^{j} \mid x^{n}: \boldsymbol{\theta}{Y \mid x^{1}}\right) \ P\left(\boldsymbol{\theta}{Y \mid x^{0}}\right) \prod_{j: x^{j}=x^{0}} P\left(y^{j} \mid x^{j}: \boldsymbol{\theta}_{Y \mid x^{0}}\right)
\end{array}




调查的抽样理论 | Sampling Theory of Surveys 代写 STATS 3003 代考

0
Posted on by

这是一份adelaide阿德莱德大学 STATS 3003 作业代写的成功案

调查的抽样理论 | Sampling Theory of Surveys 代写 STATS 3003 代考
问题 1.

a Suppose we ignore the fpc of a modcl-based estimator. Find
$$
V_{M}\left(\sum_{i \in S} \sum_{j \in S_{i}} b_{i j} Y_{i j}\right) \text {. }
$$
b Prove (5.39). HINT: Let
$$
c_{i j}= \begin{cases}b_{i j}-1 & \text { if } i \in \mathcal{S} \text { and } j \in \mathcal{S}{i} . \ -1 & \text { otherwise. }\end{cases} $$ Then, $\hat{T}-T=\sum{i=1}^{N} \sum_{j=1}^{M_{i}} c_{i j} Y_{i j}$.


证明 .

(Requires linear aIgebra and calculus.) Although $\hat{T}{r}$ is unbiased for model Ml, constructing an estimator with smaller variance is possible. Let $$ c{k}=\frac{m_{k}}{1+\rho\left(m_{k}-1\right)}
$$
and
$$
\hat{T}{\text {opt }}=\sum{i \in S} \sum_{j \in S_{i}} \frac{c_{i}}{m_{i}}\left[\rho M_{i}+\frac{K-\rho \sum_{k \in S} c_{k} \cdot M_{k}}{\sum_{k \in S} c_{k}}\right] Y_{i j}
$$

英国论文代写Viking Essay为您提供实分析作业代写Real anlysis代考服务

STATS 3003 COURSE NOTES ：

Then, for one-stage pps sampling, $t_{i} / \psi_{i}=K \bar{y}{i}$, so $$ \begin{aligned} &\hat{t}{\psi}=\frac{K}{n} \sum_{i=1}^{N} Q_{i} \bar{y}{i} \ &\hat{\hat{y}}{\psi}=\frac{1}{n} \sum_{i=1}^{N} Q_{i} \bar{y}_{i}
\end{aligned}
$$