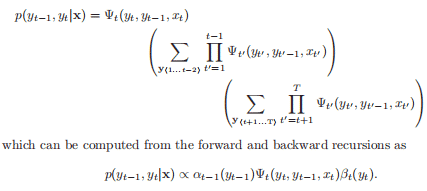这是一份贝叶斯统计推断作业代写的成功案
We will use $\theta_{X_{i} \mid \mathrm{Pa}{i}}$ to denote the subset of parameters that determine $P\left(X{i} \mid \mathrm{Pa}{i}\right)$. In the case where the parameters are disjoint (each CPD is parameterized by a separate set of parameters that do not overlap; this allows us to maximize each parameter set independently. We can write the likelihood as follows: $$ L\left(\boldsymbol{\theta}{\mathcal{G}}: \mathcal{D}\right)=\prod_{i=1}^{n} L_{i}\left(\boldsymbol{\theta}{X{i} \mid \mathbf{P a}{i}}: \mathcal{D}\right) $$ where the local likelihood function for $X{i}$ is
$$
L_{i}\left(\theta_{X_{i} \mid \mathrm{Pa}{i}}: \mathcal{D}\right)=\prod{j=1}^{m} P\left(x_{i}^{j} \mid \mathbf{p a}{i}^{j}: \theta{X_{i} \mid \mathrm{Pa}{i}}\right) . $$ The simplest parameterization for the CPDs is as a table. Suppose we have a variable $X$ with parents $\boldsymbol{U}$. If we represent that CPD $P(X \mid \boldsymbol{U})$ as a table, then we will have a parameter $\theta{x \mid u}$ for each combination of $x \in \operatorname{Val}(X)$ and $\boldsymbol{u} \in \operatorname{Val}(\boldsymbol{U})$. In this case, we can write the local likelihood function as follows:

CS 57800/ 3860/COMP 540 001/COMP_SCI 396/STAT3888/YCBS 255COURSE NOTES :
$$
P(\mathcal{G} \mid \mathcal{D})=\frac{P(\mathcal{D} \mid \mathcal{G}) P(\mathcal{G})}{P(\mathcal{D})}
$$
where, as usual, the denominator is simply a normalizing factor that does not help distinguish between different structures. Then, we define the Bayesian score as
$$
\operatorname{score}{B}(\mathcal{G}: \mathcal{D})=\log P(\mathcal{D} \mid \mathcal{G})+\log P(\mathcal{G}), $$ The ability to ascribe a prior over structures gives us a way of preferring some structures over others. For example, we can penalize dense structures more than sparse ones. It turns out, however, that this term in the score is almost irrelevant compared to the second term. This first term, $P(\mathcal{D} \mid \mathcal{G})$ takes into consideration our uncertainty over the parameters: $$ P(\mathcal{D} \mid \mathcal{G})=\int{\Theta_{\mathcal{G}}} P\left(\mathcal{D} \mid \theta_{\mathcal{G}}, \mathcal{G}\right) P\left(\theta_{\mathcal{G}} \mid \mathcal{G}\right) d \boldsymbol{\theta}_{\mathcal{G}}
$$