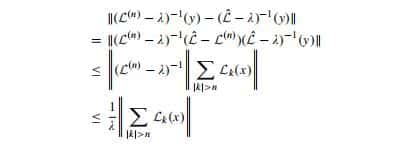这是一份warwick华威大学ST227-10 的成功案例
Let $\left(\mathbf{u}{t}\right){0 \leq t \leq T}$ be an $m$-dimensional process and
$$
\begin{aligned}
&\mathbf{a}:[0, T] \times \Omega \rightarrow \mathbb{R}^{m}, \mathbf{a} \in \mathcal{C}{1 \mathbf{w}}([0, T]) \ &b:[0, T] \times \Omega \rightarrow \mathbb{R}^{m n}, b \in \mathcal{C}{1 \mathbf{w}}([0, T])
\end{aligned}
$$
The stochastic differential $d \mathbf{u}(t)$ of $\mathbf{u}(t)$ is given by
$$
d \mathbf{u}(t)=\mathbf{a}(t) d t+b(t) d \mathbf{W}(t)
$$
if, for all $0 \leq t_{1}<t_{2} \leq T$
$$
\mathbf{u}\left(t_{2}\right)-\mathbf{u}\left(t_{1}\right)=\int_{t_{1}}^{t_{2}} \mathbf{a}(t) d t+\int_{t_{1}}^{t_{2}} b(t) d \mathbf{W}(t)
$$

ST227-10 COURSE NOTES :
Let $A$ be a nonempty subset of a metric space $(X, d)$. Define
$$
d_{A}(x):=\inf {d(x, a): a \in A}, \quad x \in X .
$$
Then $d_{A}$ is continuous. (Geometrically, we think of $d_{A}(x)$ as the distance of $x$ to $A$.)
We give a proof even though it is easy, because of the importance of this result. Let $x, y \in X$ and $a \in A$ be arbitrary. We have, from the triangle inequality $d(a, x) \leq d(a, y)+d(y, x)$,
$$
\begin{aligned}
&d(a, y) \geq d(a, x)-d(y, x) \
&d(a, y) \geq d_{A}(x)-d(y, x)
\end{aligned}
$$
The inequality says that $d_{A}(x)-d(y, x)$ is a lower bound for the set ${d(a, y): a \in A}$. Hence the greatest lower bound of this set, namely, $\inf {d(a, y)=a \in \backslash A} n d$ is greater than or equal to this lower bound, that is,
$$
d_{A}(y) \geq d_{A}(x)-d(y, x)
$$