这是一份oxford牛津大学作业代写的成功案例
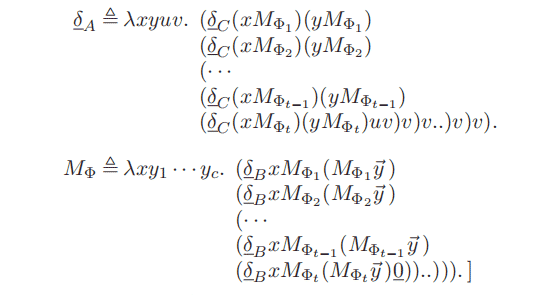

In this subsection we work with the Church variant of $\lambda_{\rightarrow}^{0}$ having one atomic type 0 , rather than with $\lambda_{\rightarrow}^{\mathbb{A}}$, having an arbitrary set of atomic types. We will write $\pi=\pi^{0}$. The reader is encouraged to investigate which results do generalize to $\mathbb{T}^{\mathbb{A}}$.
Let $\mathcal{M}={\mathcal{M}(A)}_{A \in \mathbb{}}$ be a family of non-empty sets indexed by types $A \in \mathbb{T}$.
(i) $\mathcal{M}$ is called a type structure for $\boldsymbol{\lambda}_{\rightarrow}^{0}$ if
$$
\mathcal{M}(A \rightarrow B) \subseteq \mathcal{M}(B)^{\mathcal{M}(A)}
$$
Here $X^{Y}$ denotes the collection of set-theoretic functions
$$
{f \mid f: Y \rightarrow X} .
$$
Let $X$ be a set. The full type structure $\mathcal{M}$ over the ground set $X$ defined in was specified by
$$
\begin{aligned}
\mathcal{M}(0) & \triangleq X \
\mathcal{M}(A \rightarrow B) & \triangleq \mathcal{M}(B)^{\mathcal{M}(A)}, \quad \text { for all } A, B \in \mathbb{\pi} .
\end{aligned}
$$

Oxford COURSE NOTES :
Let $\mathcal{M}$ be a typed applicative structure. A layered non-empty subfamily of $\mathcal{M}$ is a family $\Delta={\Delta(A)}_{A \in \pi}$ of sets, such that the following holds
$$
\forall A \in \Pi . \emptyset \neq \Delta(A) \subseteq \mathcal{M}(A) .
$$
$\Delta$ is called closed under application if
$$
f \in \Delta(A \rightarrow B), g \in \Delta(A) \Rightarrow f g \in \Delta(B) .
$$
$\Delta$ is called extensional if
$$
\forall A, B \in \pi \forall f, g \in \Delta(A \rightarrow B) \cdot[[\forall a \in \Delta(A) . f a=g a] \Rightarrow f=g] .
$$