这是一份PSU宾夕法尼亚州立大学STAT 505作业代写的成功案
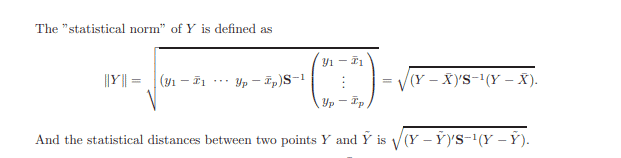

问题 1.
\begin{aligned}
&\text { Wilks’ lambda }=\prod_{i=1}^{f} \frac{1}{1+\tau_{i}}=\frac{|\mathbf{E}|}{|\mathbf{E}+\mathbf{H}|} \
&\text { Piliai’stracc }=\sum_{i=1}^{s} \frac{\eta_{1}}{1+\tau_{i}}=\operatorname{tr}\left[\mathbf{H}(\mathbf{H}+\mathbf{E})^{-1}\right]
\end{aligned}
证明 .
\begin{gathered}
\text { Hotelling-Lawley trace }=\sum_{i=1}^{\pi} \eta_{i}=\mathrm{tr}{\left[\mathrm{HE}^{-1}\right]} \ \text { Roy’s greatest root }=\frac{\eta{1}}{1+\eta_{1}}
\end{gathered}

STAT 505COURSE NOTES :
\begin{array}{ll}
\lambda_{1}=5.83, & \mathbf{e}{1}^{\prime}=[383,-924,0] \ \lambda{2}=2.00, & \mathbf{e}{2}^{\prime}=[0,0,1] \ \lambda{3}=0.17, & \mathbf{e}_{3}^{\prime}=[.924, .383,0]
\end{array}