这是一份UCL伦敦大学学院PHAS00029作业代写的成功案
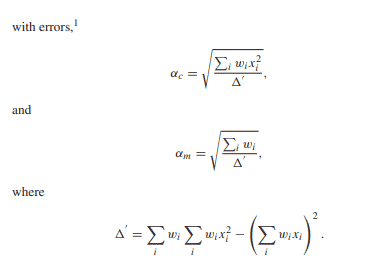

\begin{gathered}
m=\frac{\sum_{i} w_{i} \sum_{i} w_{i} x_{i} y_{i}-\sum_{i} w_{i} x_{i} \sum_{i} w_{i} y_{i}}{\sum_{i} w_{i} \sum_{i} w_{i} x_{i}^{2}-\left(\sum_{i} w_{i} x_{i}\right)^{2}} \
\alpha_{m}=\sqrt{\frac{\sum_{i} w_{i}}{\sum_{i} w_{i} \sum_{i} w_{i} x_{i}^{2}-\left(\sum_{i} w_{i} x_{i}\right)^{2}}}
\end{gathered}
\begin{aligned}
c &=\frac{\sum_{i} w_{i} x_{i}^{2} \sum_{i} w_{i} y_{i}-\sum_{i} w_{i} x_{i} \sum_{i} w_{i} x_{i} y_{i}}{\sum_{i} w_{i} \sum_{i} w_{i} x_{i}^{2}-\left(\sum_{i} w_{i} x_{i}\right)^{2}} \
\alpha_{c} &=\sqrt{\frac{\sum_{i} w_{i} x_{i}^{2}}{\sum_{i} w_{i} \sum_{i} w_{i} x_{i}^{2}-\left(\sum_{i} w_{i} x_{i}\right)^{2}}}
\end{aligned}

PHAS00029 COURSE NOTES :
$$
\begin{array}{r}
f\left(x_{1}+h\right) \approx f\left(x_{1}\right)+f^{\prime}\left(x_{1}\right) h, \
\therefore f\left(x_{1}\right)+f^{\prime}\left(x_{1}\right) h \approx 0, \
\therefore h \approx-\frac{f\left(x_{1}\right)}{f^{\prime}\left(x_{1}\right)} .
\end{array}
$$
This allows us to write down a second approximation to the zero crossing:
$$
x_{2}=x_{1}-\frac{f\left(x_{1}\right)}{f^{\prime}\left(x_{1}\right)} .
$$
The process can be repeated to obtain successively closer approximations. If after $s$ iterations the approximate solution is $x_{s}$ then the next iteration is $x_{s+1}$, and these quantities are related via the relation:
$$
x_{s+1}=x_{s}-\frac{f\left(x_{s}\right)}{f^{\prime}\left(x_{s}\right)} .
$$