这是一份andrews圣安德鲁斯大学 MT3504作业代写的成功案例
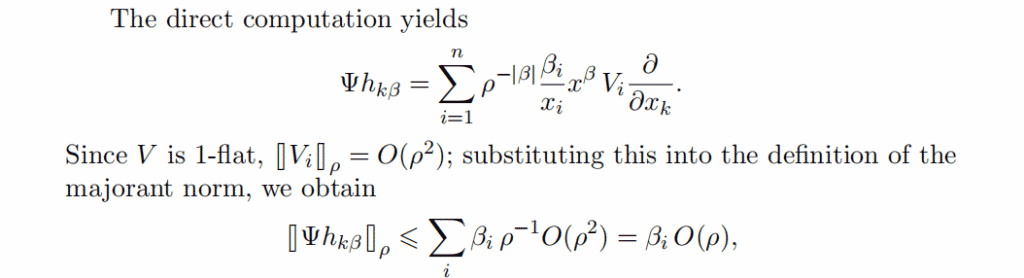
$$
x^{2} \frac{\partial}{\partial x}+(y-x) \frac{\partial}{\partial y}
$$
has vertical hyperbolic direction $\mathbb{C} \cdot(0,1)$ and the central direction $\mathbb{C} \cdot(1,1)$. The central manifold, if it exists, must be represented as the graph of the function $y=\varphi(x), \varphi(x)=x+\sum_{k \geqslant 2} c_{k} x^{k}$. However, this series diverges, as was noticed already by L. Euler. Indeed, the function $\varphi$ must be solution to the differential equation
$$
\frac{d \varphi}{d x}=\frac{\varphi(x)-x}{x^{2}}
$$
which implies the recurrent formulas for the coefficients,
$$
k c_{k}=c_{k+1}, \quad k=1,2, \ldots, \quad c_{1}=1 .
$$
The factorial series with $c_{k}=(k-1)$ ! has zero radius of convergence, hence no analytic central manifold exists.

MT3504 COURSE NOTES :
$$
i\left(a^{\prime}, S^{\prime}, \mathcal{F}^{\prime}\right)=i(a, S, \mathcal{F})-1 \text {. }
$$
Proof. The Pfaffian equation $\omega=0$ in suitable local coordinates takes the form
$$
\frac{d y}{d x}=r(x) y+\cdots, \quad x \in(\mathbb{C}, 0),
$$
where the dots denote meromorphic terms divisible by $y^{2}$ and $r(x)$ is a meromorphic function whose residue is $i(0, D, \mathcal{F})$.
Blowing up means introducing the new variable $z=y / x$ linearly depending on $y$. Changing the variable in the above equation (i.e., applying a meromorphic gauge transform in the terminology of Chapter III) yields after linearization on ${y=0}$ the differential equation
$$
\frac{d z}{d x}=r^{\prime}(x) z, \quad r^{\prime}(x)=r(x)-\frac{1}{x} .
$$