这是一份YORK约克大学MAT00001C作业代写的成功案例
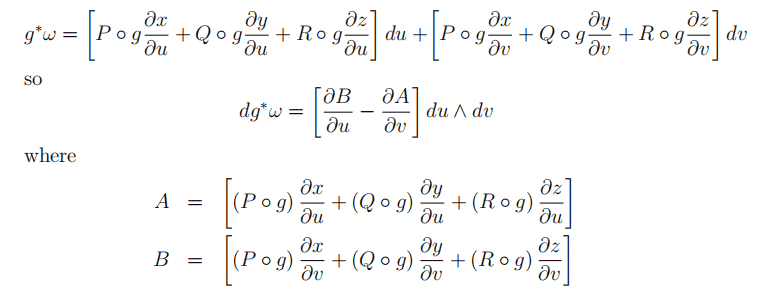

This is
$$
\left[\left[\begin{array}{c}
R \circ g \
-Q \circ g \
P \circ g
\end{array}\right] \cdot\left[\left[\frac{\partial g}{\partial u}\right] \times\left[\frac{\partial g}{\partial v}\right]\right]\right] d u \wedge d v
$$
(The permutation of the $P, Q, R$ (and the minus sign) come from the way the $d x \wedge d y$ acts on a piece of surface normal to the $(d) z$ direction.)
We can rewrite this as
$$
\left|\frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v}\right|\left[\left[\begin{array}{c}
R \circ g \
-Q \circ g \
P \circ g
\end{array}\right] \cdot \hat{\boldsymbol{n}}[u, v]\right] \quad d u \wedge d v
$$
where $\hat{\boldsymbol{n}}[u, v]$ is the unit normal to the surface at $g\left[\begin{array}{l}u \ v\end{array}\right]$, and
$$
\left|\frac{\partial g}{\partial u} \times \frac{\partial g}{\partial v}\right|
$$
is the “area stretching factor”.
We have that
$$
\int_{g\left(I^{2}\right)} \omega
$$

BMAT00001C COURSE NOTES :
is the limit of the sums of values of $\omega$ on small elements of the surface $g\left(I^{2}\right)$. Suppose $g$ takes a rectangle $\triangle u \times \triangle v$ in $I^{2}$ to a (small) piece of the surface. $\omega$ at $g\left[\begin{array}{l}u \ v\end{array}\right]$ is, say,
$$
P d x \wedge d y+Q d x \wedge d z+R d y \wedge d z
$$
and the unit normal to the surface is $\hat{\boldsymbol{n}}[u, v]$ (located at $\left.g\left[\begin{array}{l}u \ v\end{array}\right]\right)$.
Write $\hat{\boldsymbol{n}}[u, v]$ as
$$
\left[\begin{array}{l}
\hat{n} x \
\hat{n} y \
\hat{n} z
\end{array}\right]
$$