这是一份YORK约克大学MAT00004C作业代写的成功案例
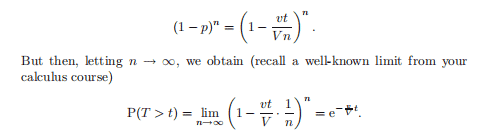
We know from integral calculus that for $0 \leq a \leq b \leq 1$
$$
\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{b} \frac{1}{2 \sqrt{x}} \mathrm{~d} x=\sqrt{b}-\sqrt{a}
$$
Hence $\int_{-\infty}^{\infty} f(x) \mathrm{d} x=\int_{0}^{1} 1 /(2 \sqrt{x}) \mathrm{d} x=1$ (so $f$ is a probability density function-nonnegativity being obvious), and
\begin{aligned}
\mathrm{P}\left(10^{-4} \leq X \leq 10^{-2}\right) &=\int_{10^{-4}}^{10^{-2}} \frac{1}{2 \sqrt{x}} \mathrm{~d} x \
&=\sqrt{10^{-2}}-\sqrt{10^{-4}}=10^{-1}-10^{-2}=0.09
\end{aligned}

MAT00004C COURSE NOTES :
Suppose $U$ has a $U(0,1)$ distribution. To construct a $\operatorname{Ber}(p)$ random variable for some $0<p<1$, we define
$$
X= \begin{cases}1 & \text { if } U<p \ 0 & \text { if } U \geq p\end{cases}
$$
so that
$$
\begin{aligned}
&\mathrm{P}(X=1)=\mathrm{P}(U<p)=p \
&\mathrm{P}(X=0)=\mathrm{P}(U \geq p)=1-p
\end{aligned}
$$
This random variable $X$ has a Bernoulli distribution with parameter $p$.
QUICK EXERCISE 6.2 A random variable $Y$ has outcomes 1,3 , and 4 with the following probabilities: $\mathrm{P}(Y=1)=3 / 5, \mathrm{P}(Y=3)=1 / 5$, and $\mathrm{P}(Y=4)=$ 1/5. Describe how to construct $Y$ from a $U(0,1)$ random variable.