这是一份umass麻省大学 STAT 515作业代写的成功案例
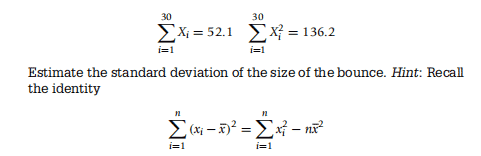

We are being asked to construct a $100(1-\alpha)$ confidence interval estimate, with $\alpha=0.10$ in part (a) and $\alpha=0.01$ in part (b). Now
$$
z_{0.05}=1.645 \text { and } z_{0.005}=2.576
$$
and so the 90 percent confidence interval estimator is
$$
\bar{X} \pm 1.645 \frac{\sigma}{\sqrt{n}}
$$
and the 99 percent confidence interval estimator is
$$
\bar{X} \pm 2.576 \frac{\sigma}{\sqrt{n}}
$$
For the data of Example 8.5, $n=10, \bar{X}=19.3$, and $\sigma=3$. Therefore, the 90 and 99 percent confidence interval estimates for $\mu$ are, respectively,
$$
19.3 \pm 1.645 \frac{3}{\sqrt{10}}=19.3 \pm 1.56
$$
and
$$
19.3 \pm 2.576 \frac{3}{\sqrt{10}}=19.3 \pm 2.44
$$

STAT516 COURSE NOTES :
$$
\bar{X} \pm 1.96 \frac{\sigma}{\sqrt{n}}
$$
Since the length of this interval is
$$
\text { Length of interval }=2(1.96) \frac{\sigma}{\sqrt{n}}=3.92 \frac{\sigma}{\sqrt{n}}
$$
we must choose $n$ so that
$$
\frac{3.92 \sigma}{\sqrt{n}} \leq b
$$
or, equivalently,
$$
\sqrt{n} \geq \frac{3.92 \sigma}{b}
$$
Upon squaring both sides we see that the sample size $n$ must be chosen so that
$$
n \geq\left(\frac{3.92 \sigma}{b}\right)^{2}
$$