这是一份 Imperial帝国理工大学 PHYS96019作业代写的成功案例
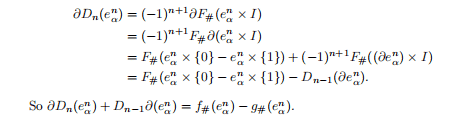

$$
G=P P \cup P x_{2} P \cup \ldots \cup P x_{p} P,
$$
where $x_{1}=e$ has been omitted. Let there be $a_{g}$ left cosets of $P$ in $P x_{j} P$. We have
$$
a_{j}=\left[x_{j}^{-1} P x_{j}: x_{j}^{-1} P x_{j} \cap P\right]
$$
$$
x_{j}^{-1} P x_{j}=\text { order } p=p^{i} \text {. }
$$
Hence $a_{j}=1$ or $p t, t \geq 1$. Now $a_{1}=1$ for the double coset $P P=P .$ Also $[G: P]=a_{1}+a_{2}+\ldots+a_{p}$. Now $p \mid[G: P]$, since $[G: P]=p^{m-i} s$, and $i \leqq(m-1)$. Thus the number of $a_{j}$ equal to 1 must be a non-zero multiple of $p$. Now $a_{j}=1$ if and only if
$$
x_{j}^{-1} P x_{j}=x_{j}^{-1} P_{x} \cap P \leftrightarrow x_{j}^{-1} P x_{j} \subset P \leftrightarrow x_{j}^{-1} P_{x}=P
$$

PHYS96019 COURSE NOTES :
Let $H=\langle h\rangle$ and $K=\langle k\rangle$. Then
$$
[h, k]=h^{-1}\left(k^{-1} h k\right) \in H,
$$
since $H$ is normal. But also
$$
[h, k]=\left(h^{-1} k^{-1} h\right) k \in K,
$$
since $K$ is normal. Thus
$$
[h, k]=h^{-1} k^{-1} h k \in H \cap K={e} .
$$
Hence $\quad h k=k h$.
By theorem $2.8 .1$ (5),
$$
O(h k)=p q .
$$