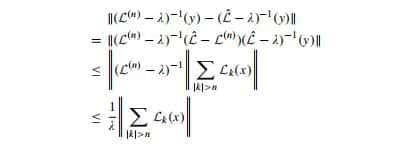
$$
\phi_{k}(x)=\sum_{m=1}^{N^{\prime}} L_{k}^{(m)^{*}} x L_{k}^{(m)}, \text { for all } x \in \mathcal{A} .
$$
Here the Linbladian $\mathcal{L}^{\phi}$ corresponding to the partial state $\phi_{0}$ is formally given by
$$
\mathcal{L}^{\phi}(x)=\sum_{k \in \mathbb{Z}^{d}} \mathcal{L}_{k}^{\phi}(x),
$$
where
$$
\mathcal{L}{k}^{\phi}(x)=\phi{k}(x)-x=\frac{1}{2} \sum_{m=1}^{N^{\prime}}\left[L_{k}^{(m)^{}}, x\right] L_{k}^{(m)}+L_{k}^{(m)^{}}\left[x, L_{k}^{(m)}\right]
$$

MATH0060 COURSE NOTES :
for all $\alpha \in I$, whenever $v \notin J_{0}$. Fixing this $J_{0}$, we choose $I_{0}$ to be the union of $I_{v, n}, v \in J_{0}, n=1,2, \cdots, \infty$, such that
$\left\langle e\left(g^{t}+\frac{1}{n}\left(H_{I} P R_{\Delta}\right){e{\nu}, v e e\left(g_{t}\right)}\right), k_{\alpha}\right\rangle=0=\left\langle k_{\alpha}, e\left(f^{t}+\frac{1}{n}\left(H_{t}^{\prime} P S_{\Delta^{\prime}}\right){e{\nu}, u e\left(f_{t}\right)}\right)\right\rangle$ for all $\alpha \notin I_{v, n}$ when $n<\infty$, and
$$
\left\langle e\left(g^{t}\right), k_{\alpha}\right\rangle=0=\left\langle k_{\alpha}, e\left(f^{t}\right)\right\rangle \text { for } \alpha \notin I_{v, \infty}
$$
We now have
$$
\left\langle H_{l} a_{R}^{\dagger}(\Delta)(v e(g)), H_{t}^{\prime} a_{S}^{\dagger}\left(\Delta^{\prime}\right)(u e(f))\right\rangle
$$