这是一份imperial帝国理工大学 MATH96018/97027/97104作业代写的成功案例
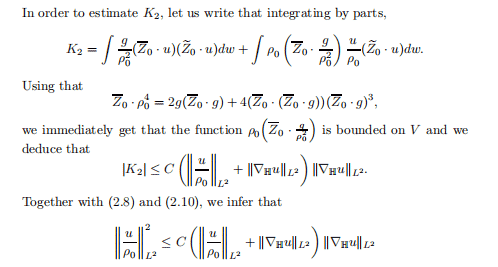
uniformly on each compact set in the $(\zeta, \varepsilon)$ space as $y$ tends to infinity in any closed subsector of the open sector,
$$
|\arg y|<\frac{3 \pi}{5}
$$
moreover
$$
E_{3}(y ; \zeta, \varepsilon)=\frac{2}{5} y^{5 / 2}+\zeta y^{1 / 2}
$$
and $B_{3, N}$ are polynomials in $(\zeta, \varepsilon)$.
We note that, setting
$$
\omega=\exp \left[i \frac{2}{5} \pi\right]
$$
and
$$
\mathscr{Y}{3, k}(y ; \zeta, \varepsilon)=\mathscr{Y}{3}\left(\omega^{-k} y ; \omega^{-2 k} \zeta, \omega^{-3 k} \varepsilon\right),
$$

MATH96018/97027/97104 COURSE NOTES :
Let us now consider the above equation in a neighborhood of $\left(0, \zeta_{0}\right)$. There exists a positive $\delta$ such that each root of the equation
$$
C_{0}(\zeta, \varepsilon)=0
$$
for some positive integer $p$, is a holomorphic function of $\varepsilon^{1 / p}$, for $0<|\varepsilon|<\delta$, that is
$$
\zeta(\varepsilon)=\zeta_{0}+\sum_{j=0}^{\infty} c_{j}\left(\varepsilon^{1 / p}\right)^{j}=g\left(\varepsilon^{1 / p}\right)
$$
This is actually a consequence of Theorem $3.2 .6$ in $[6]$, observing that $\gamma(\zeta, \varepsilon) \neq 0$ implies that the function $g$ has no polar singularity at the origin.
As a matter of fact the function $g$ is holomorphic in a full neighborhood of the origin so that $\zeta\left(\eta^{p}\right)=g(\eta)$, which is a well-defined holomorphic function of $\eta$.