这是一份umass麻省大学 MATH 456作业代写的成功案例
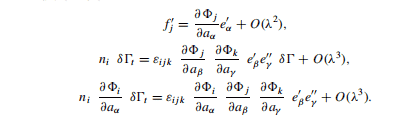

As for $n=n_{t}(a, t)$, we see that
$$
\left(a^{\prime}-a\right) \wedge\left(a^{\prime \prime}-a\right)=e^{\prime} \wedge e^{\prime \prime}\left(=O\left(\lambda^{2}\right)\right)=n_{0} \delta \Gamma_{0}+O\left(\lambda^{3}\right),
$$
where $n_{0}=n_{0}(a, t)$ and $\delta \Gamma_{0}=\delta \Gamma_{0}(a, t)$ is the area of the parallelepiped constructed over $e^{\prime}$ and $e^{\prime \prime}$; hence
$$
n_{i} \frac{\partial \Phi_{i}}{\partial a_{\alpha}} \delta \Gamma_{t}=n_{0 \alpha} \operatorname{det} \mathbf{F} \delta \Gamma_{0}+O\left(\lambda^{3}\right),
$$
and, in vector form,
$$
n_{0} \operatorname{det} \mathbf{F} \delta \Gamma_{0}=\mathbf{F}^{T} \cdot n_{t} \delta \Gamma_{t}+O\left(\lambda^{3}\right) .
$$
Since $n_{0}$ has norm 1 , this also gives
$$
(\operatorname{det} \mathbf{F})^{2}\left(\delta \Gamma_{0}\right)^{2}=n_{t}^{T} \cdot \mathbf{F} \cdot \mathbf{F}^{T} \cdot n_{t}\left(\delta \Gamma_{t}\right)^{2}+O\left(\lambda^{5}\right),
$$
or, since $B=\mathbf{F} \cdot \mathbf{F}^{T}$ (see Section 5.1),
$$
(\operatorname{det} \mathbf{F})^{2}\left(\delta \Gamma_{0}\right)^{2}=n_{t}^{T} \cdot B \cdot n_{t}\left(\delta \Gamma_{t}\right)^{2}+O\left(\lambda^{5}\right) .
$$

MMATH 456 COURSE NOTES :
If we know that
$$
\frac{d}{d t} \int_{\Omega_{t}^{\prime}} C d x=\int_{\Omega_{t}^{\prime}} f d x, \quad \forall \Omega_{t}^{\prime} \subset \Omega_{t}
$$
then
$$
\frac{\partial C}{\partial t}+\operatorname{div}(C U)=f \quad \text { in } \Omega_{t}^{i}, \quad i=1,2,
$$
and
$$
\int_{\Sigma_{i}^{\prime}}[C V] \cdot N d \Gamma=0, \quad \forall \Sigma_{t}^{\prime} \subset \Sigma_{t} ;
$$
hence,
$$
[C V] \cdot N=0 \text { on } \Sigma_{t} .
$$
When $C$ is a scalar, setting $v=V \cdot N$, we rewrite the last relation as
$$
(C v){2}-(C v){1}=0 .
$$