Assignment-daixieTM为您提供布里斯托大学University of Bristol Advanced Quantum Physics PHYSM3416高级量子物理学代写代考和辅导服务!
Instructions:
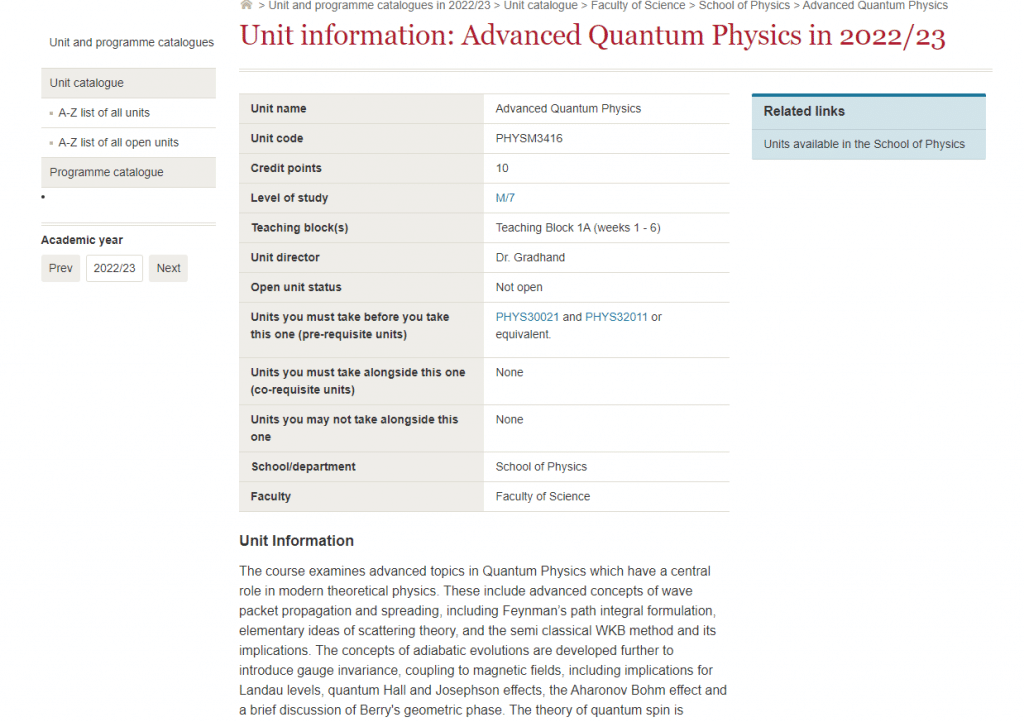
The Feynman path integral formulation is a powerful tool for understanding quantum mechanics, and it allows for the calculation of transition probabilities between states. Scattering theory is important for understanding the interaction of particles and can be used to predict the behavior of atoms, molecules, and nuclei.
The semi-classical WKB method is useful for approximating solutions to quantum mechanical problems, particularly when the potential is slowly varying. Adiabatic evolutions are important for understanding the behavior of systems that change slowly over time, such as quantum computers.
The addition of angular momenta is an important concept in quantum mechanics, and the Clebsch Gordan algebra provides a mathematical framework for understanding it. The Bloch sphere is a useful tool for representing spins, and it has applications in quantum computing and magnetic resonance imaging.
The course also covers magnetic fields and their effects on quantum systems, including Landau levels, the quantum Hall effect, and the Aharonov-Bohm effect. Finally, the discussion of Berry’s geometric phase provides a deeper understanding of the behavior of quantum systems in the presence of external forces.
Overall, this course seems like an excellent opportunity to explore advanced topics in quantum physics and develop a deeper understanding of the behavior of quantum systems.
Here we discuss an angular momentum algebra using the one-dimensional harmonic oscillator. Throughout this question we will set $\hbar=1$ (to save ink). Consider a pair of creation and annihilation operators $\hat{a}^{\dagger}$ and $\hat{a}$ satisfying $\left[\hat{a}, \hat{a}^{\dagger}\right]=1$ and a number basis of states $$ |n\rangle=\frac{1}{\sqrt{n !}}\left(\hat{a}^{\dagger}\right)^n|0\rangle, \quad \hat{N}|n\rangle \equiv \hat{a}^{\dagger} \hat{a}|n\rangle=n|n\rangle . $$ (a) Now define, with $j$ a positive integer, the operators $$ J_z=-j+\hat{N}, \quad J_{+}=\hat{a}^{\dagger} \sqrt{2 j-\hat{N}}, \quad J_{-}=J_{+}^{\dagger}=\sqrt{2 j-\hat{N}} \hat{a} . $$ Verify that these operators define an angular momentum algebra. Note: You should not have to expand the square roots in your manipulations. These operators are defined only on states for which the argument of the square root is not negative.
(a) To show that the operators $J_z, J_+, J_-$ define an angular momentum algebra, we need to verify that they satisfy the commutation relations \begin{align} [J_z, J_{\pm}] &= \pm J_{\pm}, \ [J_+, J_-] &= 2J_z. \end{align}
First, we have \begin{align} [J_z, J_+] &= [(-j + \hat{N}), (\hat{a}^\dagger \sqrt{2j – \hat{N}})] \ &= \hat{a}^\dagger [(-j + \hat{N}), \sqrt{2j – \hat{N}}] + [(j – \hat{N}), \hat{a}^\dagger] \sqrt{2j – \hat{N}} \ &= \hat{a}^\dagger (-1/2) [\hat{N} – 2j, \sqrt{2j – \hat{N}}] + \hat{a}^\dagger \sqrt{2j – \hat{N}} \ &= \hat{a}^\dagger (-1/2) (\sqrt{2j – \hat{N}} [\hat{N}, \sqrt{2j – \hat{N}}] – [\hat{N}, \sqrt{2j – \hat{N}}]\sqrt{2j – \hat{N}}) + \hat{a}^\dagger \sqrt{2j – \hat{N}} \ &= \hat{a}^\dagger (\sqrt{2j – \hat{N}}) + \hat{a}^\dagger (\sqrt{2j – \hat{N}}) \ &= 2J_+, \end{align} where we have used the commutation relations $[\hat{N}, \hat{a}^\dagger] = \hat{a}^\dagger$ and $[\hat{N}, \hat{a}] = -\hat{a}$.
Next, we have \begin{align} [J_z, J_-] &= [(-j + \hat{N}), (\sqrt{2j – \hat{N}} \hat{a})] \ &= \sqrt{2j – \hat{N}} [(-j + \hat{N}), \hat{a}] + [(-j + \hat{N}), \sqrt{2j – \hat{N}}] \hat{a} \ &= -\sqrt{2j – \hat{N}} \hat{a} + \sqrt{2j – \hat{N}} \hat{a} \ &= 0. \end{align}
Finally, we have \begin{align} [J_+, J_-] &= [(\hat{a}^\dagger \sqrt{2j – \hat{N}}), (\sqrt{2j – \hat{N}} \hat{a})] \ &= \sqrt{2j – \hat{N}} [\hat{a}^\dagger, \hat{a}] \sqrt{2j – \hat{N}} \ &= (2j – \hat{N}) – \hat{N} \ &= 2J_z. \end{align}
Therefore, the operators $J_z, J_+, J_-$ define an angular momentum algebra.
(b) Construct the corresponding $J^2$ operator. Does it satisfy the proper commutation relations with the $J_i$ operators?
(b) The $J^2$ operator is defined as $J^2=J_x^2+J_y^2+J_z^2$, where $J_x$, $J_y$, and $J_z$ are the angular momentum operators. In terms of the creation and annihilation operators, we can write these operators as \begin{align} J_x &= \frac{1}{2}\left(\hat{a}^{\dagger}+\hat{a}\right), \ J_y &= \frac{1}{2i}\left(\hat{a}^{\dagger}-\hat{a}\right), \ J_z &= \frac{1}{2}\left(\hat{a}^{\dagger}\hat{a}-\frac{1}{2}\right), \end{align} where we have chosen $\hbar=1$. Then, we can calculate $J^2$ as \begin{align} J^2 &= J_x^2+J_y^2+J_z^2 \ &= \frac{1}{4}\left(\hat{a}^{\dagger}+\hat{a}\right)^2 – \frac{1}{4}\left(\hat{a}^{\dagger}-\hat{a}\right)^2 + \frac{1}{4}\left(\hat{a}^{\dagger}\hat{a}-\frac{1}{2}\right)^2 \ &= \frac{1}{2}\left(\hat{a}^{\dagger}\hat{a}+\frac{1}{4}\right). \end{align} Note that we have used the commutation relation $\left[\hat{a}, \hat{a}^{\dagger}\right]=1$ to simplify the expression. We can check that $J^2$ commutes with $J_x$, $J_y$, and $J_z$: \begin{align} \left[J^2, J_x\right] &= \left[J^2, J_y\right] = \left[J^2, J_z\right] = 0, \end{align} so $J^2$ and $J_i$ form a set of commuting observables.
(c) Find a subset of the harmonic oscillator basis states $|n\rangle$ with $n=0,1,2, \ldots$ that forms a multiplet of $\mathbf{J}$ with angular momentum $j$. Write explicitly your $|j, m\rangle$ states in terms of the oscillator basis states. Confirm that $J_z$ and $J_{+}$act as expected on these states.
The angular momentum operators are given by $\mathbf{J}=\mathbf{r} \times \mathbf{p}$, where $\mathbf{r}$ is the position operator and $\mathbf{p}$ is the momentum operator. In one dimension, we have $\mathbf{r}=x$ and $\mathbf{p}=-i \partial / \partial x$. Therefore, the angular momentum operator can be written as
$\mathbf{J}=x p+i \hat{k}$
where $\hat{k}$ is a constant vector in the $z$ direction.
Using the creation and annihilation operators, we can write $x$ and $p$ in terms of $\hat{a}$ and $\hat{a}^{\dagger}$ as
$x=\sqrt{\frac{1}{2 \omega}}\left(\hat{a}+\hat{a}^{\dagger}\right), \quad p=-i \sqrt{\frac{\omega}{2}}\left(\hat{a}-\hat{a}^{\dagger}\right)$,
where $\omega$ is the frequency of the harmonic oscillator.
Substituting these expressions into the expression for $\mathbf{J}$, we get
$\mathbf{J}=\frac{1}{\sqrt{2 \omega}}\left[\left(\hat{a}+\hat{a}^{\dagger}\right)\left(\hat{a}-\hat{a}^{\dagger}\right)+i \hat{k}\right]$.
Let’s define the total number operator as $\hat{N}=\hat{a}^{\dagger} \hat{a}$, which counts the number of excitations in the oscillator. We can use $\hat{N}$ to label the states $|n\rangle$.
Now, we can write down the action of $\mathbf{J}^2$ and $J_z$ on the states $|n\rangle$: \begin{align} \mathbf{J}^2 |n\rangle &= j(j+1) |n\rangle, \ J_z |n\rangle &= m |n\rangle, \end{align} where $j$ and $m$ are the total angular momentum and the $z$ component of angular momentum, respectively. We want to find a subset of the states $|n\rangle$ that form a multiplet of $\mathbf{J}$ with angular momentum $j$.
To do this, we can define the raising and lowering operators
$J_{ \pm}=J_x \pm i J_y=\frac{1}{\sqrt{2}}\left[\left(\hat{a}^{\dagger}\right)^2-\hat{a}^2 \pm i\left(\hat{a}^{\dagger} \hat{a}+\hat{a} \hat{a}^{\dagger}\right)\right]$.
Using the commutation relation $[\hat{a},\hat{a}^\dagger]=1$, we can show that $[J_z,J_{\pm}]=\pm J_{\pm}$ and $[J_+,J_-]=2J_z$. Therefore, if we start with a state $|j,m\rangle$ and apply the raising operator $J_+$ repeatedly, we generate a set of states with angular momentum $j$ that are proportional to $|j,j\rangle$.
