Assignment-daixieTM为您提供伯明翰大学University of Birmingham Applied Economics and Statistics 08 29165应用经济学和统计学代写代考和辅导服务!
Instructions:
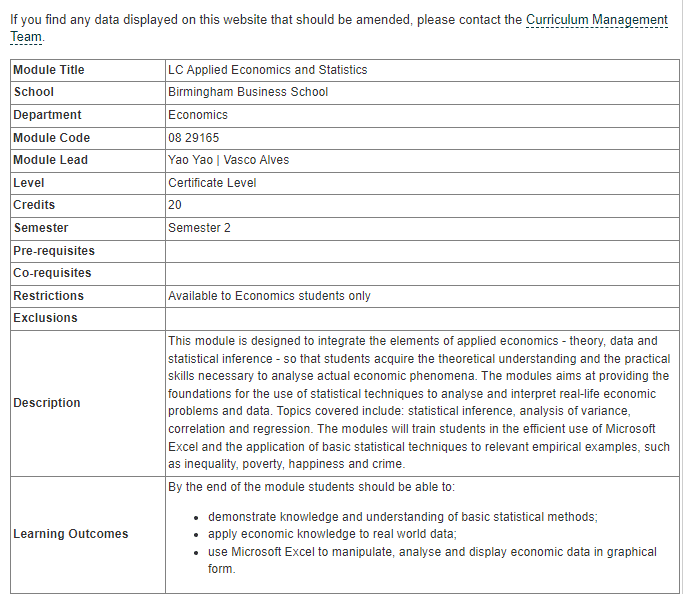
This module aims to provide a comprehensive understanding of applied economics, including both theoretical knowledge and practical skills. The focus on statistical techniques, such as analysis of variance, correlation, and regression, will enable students to interpret real-life economic problems and data with greater accuracy and efficiency.
By using Microsoft Excel, students will have a practical tool to help them apply these statistical techniques to relevant empirical examples. This could include investigating issues such as inequality, poverty, happiness, and crime, which are all important economic issues with real-world implications.
Overall, it sounds like this module will be highly beneficial for students interested in pursuing careers in economics, finance, or related fields, as well as those who simply want to develop their analytical and statistical skills.
Suppose that income $Y$ is distributed as a Pareto distribution: $f(y)=\alpha y^{-(\alpha+1)}$ for $1 \leq y$, with $\alpha>1$. (a) It is quite common to not observe all incomes, but only those that are higher than some threshold (so-called truncated variables). Assume that you observe only those individuals with an income greater than or equal to $\$ 9,000$, and their income is described by a random variable $Y^*$. How is $Y^*$ distributed?
(a) The truncated variable $Y^*$ is distributed as a Pareto distribution truncated from below at $9,000$. That is,
$f_{Y^*}(y)= \begin{cases}\frac{\alpha}{9,000^\alpha} y^{-(\alpha+1)}, & y \geq 9,000 \ 0, & \text { otherwise. }\end{cases}$
(b) Your have a sample of size $N$ drawn from the population of persons with incomes greater than or equal to $\$ 9,000$. What is the MLE of $\alpha$ ?
(b) The likelihood function for the sample $y_1, \ldots, y_N$ is given by
$\mathcal{L}(\alpha)=\prod_{i=1}^N f_{Y^*}\left(y_i\right)=\frac{\alpha^N}{9,000^{N \alpha}}\left(\prod_{i=1}^N y_i\right)^{-(\alpha+1)} \mathbb{I}{\left{y{(1)}>9,000\right}}$
where $y_{(1)}$ is the smallest observation in the sample. Since $\alpha > 1$, the log-likelihood function is
$\frac{\partial \ell(\alpha)}{\partial \alpha}=\frac{N}{\alpha}-\sum_{i=1}^N \log y_i+\frac{N}{\alpha+1}=0$
which yields the MLE of $\alpha$:
$\hat{\alpha}=\frac{N}{\sum_{i=1}^N \log \left(y_i / 9,000\right)+N}$.
(c) What is asymptotic distribution of the estimator in (b)?
(c) To derive the asymptotic distribution of the MLE, we need to calculate its variance. The second-order condition for maximizing the log-likelihood function is
$\frac{\partial^2 \ell(\alpha)}{\partial \alpha^2}=-\frac{N}{\alpha^2}-\frac{N}{(\alpha+1)^2}<0$,
which implies that the MLE is a maximum. The variance of the MLE is given by
$\operatorname{Var}(\hat{\alpha})=\left(-\frac{\partial^2 \ell(\alpha)}{\partial \alpha^2}\right)^{-1}=\frac{\hat{\alpha}^2}{N}$
By the central limit theorem, we know that $\sqrt{N}(\hat{\alpha} – \alpha_0) \rightarrow_d \mathcal{N}(0, V)$ as $N \rightarrow \infty$, where $\alpha_0$ is the true value of $\alpha$ and $V$ is the asymptotic variance of $\hat{\alpha}$. Hence, the asymptotic distribution of the MLE is
$\hat{\alpha} \sim \mathcal{N}\left(\alpha_0, \frac{\alpha_0^2}{N}\right)$.
