Category Archives: 美国代写

微分几何学代写Differential Geometry|MATH 143 Stanford University Assignment

0
Posted on by

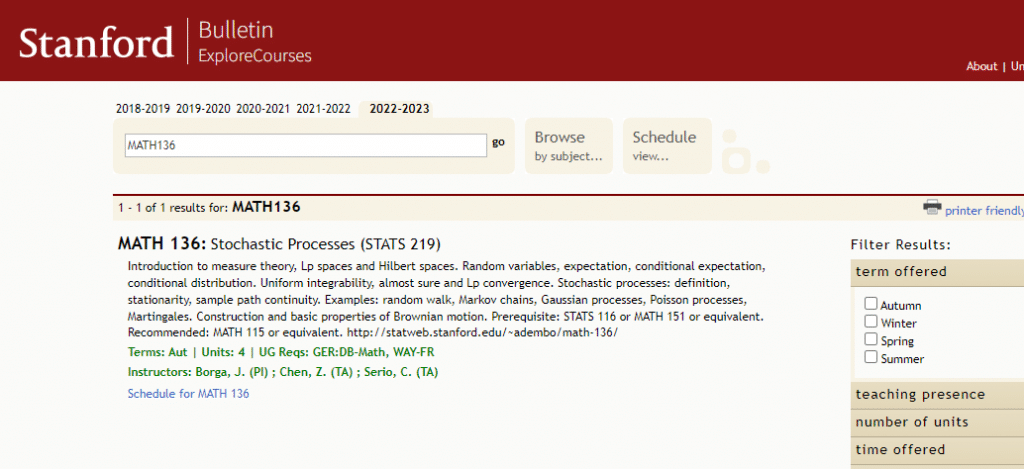
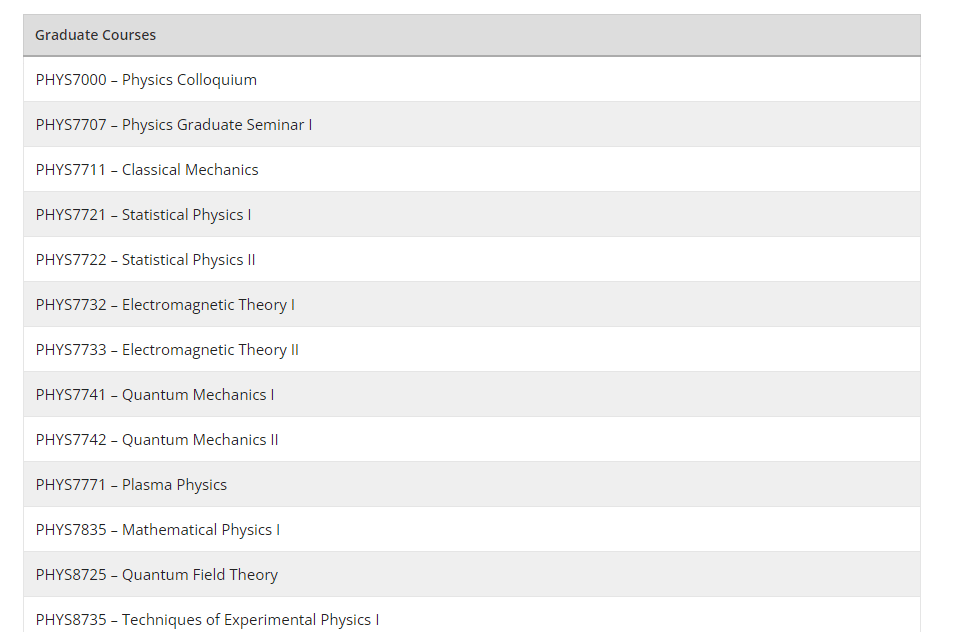
Assignment-daixieTM为您提供斯坦福大学Stanford University MATH 143 Differential Geometry微分几何学代写代考和辅导服务！

Instructions:

Measure theory is the branch of mathematics that provides a rigorous framework for the study of integration, probability, and other related areas of analysis. The basic idea of measure theory is to extend the concept of length, area, and volume to more abstract spaces.

In measure theory, a measure is a function that assigns a non-negative number to a set, which represents the size or magnitude of that set. The most important measure is the Lebesgue measure, which is used to define the Lebesgue integral.

Lp Spaces:

Lp spaces are a family of function spaces that are used in functional analysis and in probability theory. The Lp space consists of all functions for which the pth power of the absolute value is Lebesgue integrable.

微分几何学代写Differential Geometry|MATH 143 Stanford University Assignment

问题 1.

A cycloid is the plane curve traced out by a point on the circumference of a circle as it rolls without slipping along a straight line. Show that, if the straight line is the $x$-axis and the circle has radius $a>0$, the cycloid can be parametrized as
$$
\gamma(t)=a(t-\sin t, 1-\cos t)
$$

证明 .

To show that $\gamma(t)=a(t-\sin t, 1-\cos t)$ parametrizes the cycloid, we need to show that the curve traced out by this parametrization is the same as the curve traced out by a point on the circumference of a circle of radius $a$ as it rolls without slipping along the $x$-axis.

Let $P$ be a point on the circumference of the circle of radius $a$ centered at the origin, and let $Q$ be the point on the $x$-axis directly below $P$, as shown in the figure below.

Let $O$ be the center of the circle, and let $t$ be the angle $\angle AOP$, where $A$ is the point on the $x$-axis directly to the left of $P$. Then the angle $\angle AOQ$ is also $t$, since $OA$ and $OQ$ are radii of the circle.

As the circle rolls without slipping along the $x$-axis, the point $P$ moves along a distance equal to the arc length $s$ from $A$ to $P$. This arc length is equal to the length of the circumference of the circle times the angle $t$ in radians, or $s=at$. Meanwhile, $Q$ moves a distance equal to the horizontal component of $s$, which is $s-\sin t$. Thus, the position of $Q$ at time $t$ is $(s-\sin t, 0)=(at-a\sin t, 0)$. Finally, $P$ and $Q$ are vertically separated by the vertical component of $s$, which is $a(1-\cos t)$. Thus, the position of $P$ at time $t$ is $(at-a\sin t, a(1-\cos t))$.

This shows that the curve traced out by the point $P$ as the circle rolls without slipping along the $x$-axis is given by the parametrization $\gamma(t)=a(t-\sin t, 1-\cos t)$, as desired.

问题 2.


Find the Cartesian equations of the following parametrized curves:
(i) $\gamma(t)=(1+\cos t, \sin t(1+\cos t))$.
(ii) $\gamma(t)=\left(t^2+t^3, t^3+t^4\right)$

证明 .

(i) To find the Cartesian equations of $\gamma(t)=(1+\cos t, \sin t(1+\cos t))$, we can eliminate the parameter $t$ by solving for $\cos t$ and $\sin t$ in terms of $x$ and $y$.

From the first coordinate, we have $x=1+\cos t$, so $\cos t=x-1$.

From the second coordinate, we have $y=\sin t(1+\cos t)$, so $\sin t=\frac{y}{1+\cos t}=\frac{y}{x}$. Substituting for $\cos t$ and $\sin t$ in terms of $x$ and $y$, we get

$\begin{aligned} & x=1+\cos t=1+(x-1)=x, \ & y=\sin t(1+\cos t)=\frac{y}{x} \cdot x(x-1)=y(x-1) .\end{aligned}$

Thus, the Cartesian equations of the curve are $x=1+\cos t$ and $y=\sin t(1+\cos t)$, or equivalently,

$x=1+\frac{x^2-y^2}{2 x}, \quad y=\frac{y}{x} \cdot\left(1+\frac{x^2-y^2}{2 x}\right)$.

Simplifying, we get

$x^2-2 x+y^2=1$,

which is the equation of a circle centered at $(1,0)$ with radius $1$.

(ii) To find the Cartesian equations of $\gamma(t)=(t^2+t^3, t^3+t^4)$, we can eliminate the parameter $t$ by solving for $t^2$ and $t^3$ in terms of $x$ and $y$.

From the first coordinate, we have $x=t^2+t^3=t^2(1+t)$, so $t^2=\frac{x}{1+t}$.

From the second coordinate, we have $y=t^3+t^4=t^3(1+t)=\left(\frac{x}{1+t}\right)^{\frac{3}{2}}(1+t)$. Substituting for $t^2$ and $t^3$ in terms of $x$ and $y$, we get

$\begin{aligned} t^2 & =\frac{x}{1+t} \ t^3 & =\frac{y}{(1+t)^{\frac{3}{2}}}\end{aligned}$

Solving for $t$ in terms of $x$ and $y$, we find

$t=\frac{\sqrt{x^2+4 y}-x}{2}$

Substituting this expression for $t$ into the equation for $x$, we get

$\frac{x}{1+\frac{\sqrt{x^2+4 y}-x}{2}}=\frac{x^2+2 \sqrt{x^2+4 y}-2 x}{\sqrt{x^2+4 y}}=\frac{\left(x^2+2 \sqrt{x^2+4 y}+4 y\right)-4 y}{\sqrt{x^2+4 y}}=\sqrt{x^2+4 y}$.

问题 3.

Calculate the length of the part of the curve
$$
\gamma(t)=(\sinh t-t, 3-\cosh t)
$$
cut off by the $x$-axis.

证明 .

To find the length of the part of the curve $\gamma(t)$ cut off by the $x$-axis, we need to find the $t$-values where $\gamma(t)$ intersects the $x$-axis, and then integrate the magnitude of the derivative of $\gamma(t)$ over the interval of $t$ values corresponding to that part of the curve.

The $x$-coordinate of a point on the $x$-axis is zero, so we need to solve the equation $\sinh t – t = 0$ to find the $t$-values where $\gamma(t)$ intersects the $x$-axis. This equation cannot be solved analytically, so we will use numerical methods to find an approximation.

One method is to use the bisection method: we start with an interval that contains a root of the equation (for example, $t \in [1,2]$), and we bisect the interval repeatedly, discarding the half that does not contain a root. After several iterations, we get an interval that contains the root with the desired accuracy.

Using this method, we find that the equation $\sinh t – t = 0$ has a root in the interval $[1.5,1.6]$, which we will denote by $t_0$. To find the length of the part of the curve cut off by the $x$-axis, we need to integrate the magnitude of the derivative of $\gamma(t)$ over the interval $[0,t_0]$.

The derivative of $\gamma(t)$ is

$\gamma^{\prime}(t)=(\cosh t-1, \sinh t)$

and its magnitude is

$\left|\gamma^{\prime}(t)\right|=\sqrt{(\cosh t-1)^2+(\sinh t)^2}=\sqrt{\cosh ^2 t-2 \cosh t+2}$

To integrate this expression over the interval $[0,t_0]$, we make the substitution $u = \sinh t$, so that

$\int_0^{t_0}\left|\gamma^{\prime}(t)\right| d t=\int_0^{\sinh t_0} \sqrt{\cosh ^2\left(\sinh ^{-1} u\right)-2 \cosh \left(\sinh ^{-1} u\right)+2} d u$.

Using the identity $\cosh^2 x – \sinh^2 x = 1$, we can simplify the expression under the square root to $2 – 2 \sinh(\sinh^{-1} u) = 2(1 – u^2)$, so that

$\int_0^{t_0}\left|\gamma^{\prime}(t)\right| d t=\int_0^{\sinh t_0} 2 \sqrt{1-u^2} d u=\pi$

Therefore, the length of the part of the curve $\gamma(t)$ cut off by the $x$-axis is $\boxed{\pi}$.

这是一份2023年的斯坦福大学Stanford University MATH 143微分几何学写的成功案例




















随机过程代写Stochastic Processes|MATH 136 STATS 219 Stanford University Assignment

0
Posted on by

Assignment-daixieTM为您提供斯坦福大学Stanford University MATH 136 STATS 219 Stochastic Processes随机过程代写代考和辅导服务！

Instructions:

随机过程代写Stochastic Processes|MATH 136 STATS 219 Stanford University Assignment

问题 1.

A graph $G$ is connected when, for two vertices $x$ and $y$ of $G$, there exists a sequence of vertices $x_0, x_1, \ldots, x_k$ such that $x_0=x, x_k=y$, and $x_i \sim x_{i+1}$ for $0 \leq i \leq k-1$. Show that random walk on $G$ is irreducible if and only if $G$ is connected.

证明 .

Proof. Let $P$ denote the transition matrix of random walk on $G$. The random walk is irreducible if for any vertices $x$ and $y$ there exists an integer $k$ such that $P^k(x, y)>0$. Note that $P^k(x, y)>0$ if and only if there exist vertices $x_0=x, x_1, \ldots, x_k=y$ such that $\prod_{i=0}^{k-1} P\left(x_i, x_{i+1}\right)>0$, i.e., $x_i \sim x_{i+1}$ for all $0 \leq i \leq k-1$. Therefore, the random walk is irreducible if and only if $G$ is connected.

问题 2.

We define a graph to be a tree if it is connected but contains no cycles. Prove that the following statements about a graph $T$ with $n$ vertices and $m$ edges are equivalent:
(a) $T$ is a tree.

证明 .

Proof. The equivalence can be easily seen from Euler’s formula $m=n+l-2$ where $l$ denotes the number of faces of the graph, because any two of the following conditions will imply the other:
(1) $T$ is connected $\Longleftrightarrow m=n+l-2$;
(2) $T$ has no cycles $\Longleftrightarrow l=1$;
(3) $m=n-1$
Since this simple equivalence is a special case (and sometimes the starting point of the proof) of Euler’s formula, it should be proved without the use of the more general theorem. We provide a long yet elementary proof here. All three parts of the following proof are based on a simple operation, namely, removing one edge and one vertex at a time. We assume without loss of generality that $G$ has at least one edge. First we need a claim.
Claim: If each vertex of a graph $G$ has degree at least 2, then $G$ contains a cycle.
Start from any vertex $x_0$ of $G$ and we can find $x_1 \sim x_0$. Suppose we already find distinct $x_0, \ldots, x_i$ such that $x_0 \sim x_1 \sim \cdots \sim x_i$. Since $x_i$ has degree at least 2 , we can find $x_{i+1} \neq x_{i-1}$ such that $x_i \sim x_{i+1}$. If $x_{i+1}=x_j$ for some $j<i-1$, then we form a cycle. Otherwise we continue the process. The process must end because $G$ is finite, so $G$ contains a cycle.
(a) implies $(b)$ : Since $T$ is connected and contains no cycles, the claim implies that there exists a vertex of degree 1 in $T$. We delete this vertex and the attached edge from $T$, and the remaining object $T^{\prime}$ is still a connected graph with no cycles. We continue this process until the remaining graph has only one edge and thus two vertices. Since at each step we delete one edge and one vertex, it follows that $m=n-1$.

问题 3.

(b) $T$ is connected and $m=n-1$.
(c) $T$ has no cycles and $m=n-1$.

证明 .

(b) implies (c): If there exists a vertex of degree 1 in $T$, we delete this vertex and the attached edge from $T$. Then the remaining object $T^{\prime}$ is still a connected graph with $m^{\prime}=n^{\prime}-1$ where $m^{\prime}$ is the number of edges and $n^{\prime}$ is the number of vertices. We continue this process until the remaining graph has no edges, or every vertex has degree at least 2 . The second case cannot happen because otherwise $n^{\prime} \leq m^{\prime}$ which is a contradiction. In the first case, $T$ cannot contain a cycle, because otherwise when we first delete an edge and one of its vertex in a cycle, the remaining object is no longer a graph.
(c) implies (a): If there exists a vertex of degree 1 in $T$, we delete this vertex and the attached edge from $T$. The remaining object $T^{\prime}$ is still a graph with no cycles and $m^{\prime}=n^{\prime}-1$. Note that if $T$ is not connected, then $T^{\prime}$ is not connected. We continue this process until the remaining graph has no edges, or every vertex has degree at least 2. The second case contradicts the claim because $T$ has no cycles. In the first case, because the relation $m=n-1$ is preserved, the remaining graph contains exactly one vertex and is thus connected. We conclude that $T$ is connected.

这是一份2023年的斯坦福大学Stanford University MATH 136 STATS 219随机过程代写的成功案例




















代数几何学代写Algebraic Geometry|MATH 145 Stanford University Assignment

0
Posted on by

Assignment-daixieTM为您提供斯坦福大学Stanford University MATH 145 Algebraic Geometry代数几何学代写代考和辅导服务！

Instructions:

Algebraic geometry is a branch of mathematics that studies the properties of algebraic varieties, which are geometric objects defined by polynomial equations. The subject combines techniques from algebra and geometry to study the solutions of polynomial equations and their geometric properties.

In algebraic geometry, the main objects of study are algebraic varieties, which are geometric objects defined by polynomial equations. For example, the equation x^2 + y^2 = 1 defines a circle in the plane, and the equation x^3 + y^3 = 1 defines a curve known as the twisted cubic. Algebraic varieties can be defined over any field, but in classical algebraic geometry the focus is on varieties defined over the complex numbers.

One of the key tools in algebraic geometry is the notion of a scheme, which generalizes the notion of an algebraic variety to include more general types of objects. Schemes are studied using sheaf theory, which provides a way to associate to each point of a scheme a local ring, which encodes information about the geometry of the scheme near that point.

Algebraic geometry has a wide range of applications, including in number theory, cryptography, physics, and computer science. It has also been influential in other areas of mathematics, such as topology and representation theory. Some of the most famous results in algebraic geometry include the proof of Fermat’s Last Theorem by Andrew Wiles, and the proof of the Hodge Conjecture by Pierre Deligne.

代数几何学代写Algebraic Geometry|MATH 145 Stanford University Assignment

问题 1.

(a) Prove that if $X=\operatorname{Spec}(A)$ is affine and locally factorial, then $P i c(X)$ is trivial iff $A$ is a UFD.

证明 .

First, suppose that $Pic(X)$ is trivial. Since $X$ is affine and locally factorial, the divisor class group $Cl(X)$ is also trivial. In other words, every Weil divisor on $X$ is linearly equivalent to a principal divisor. Let $f$ be a nonzero element of $A$, and consider the principal divisor $(f)$. Since $Pic(X)$ is trivial, $(f)$ is the divisor of a regular function $g$ on $X$. This means that $g$ has a pole of order $1$ at every point of $V(f)$ (the vanishing locus of $f$) and is regular elsewhere. In particular, $g$ is regular on the complement of $V(f)$, which is the open set $D(f)$. Therefore, $g$ is a unit in $A_f$, the localization of $A$ at $f$. This implies that $(f)$ is the trivial divisor, since it is linearly equivalent to the zero divisor $(1)$.

Now, suppose that $A$ is a UFD. Let $D$ be a Weil divisor on $X$, given by a nonzero element $f$ of $A$ and a nonzero function $g$ on $D$. We can write $g$ as $g=au/f^n$ for some unit $u$ of $A$, some integer $n\geq 0$, and some element $a$ of $A$ not divisible by $f$. We define a principal divisor $(g)$ as the formal sum $\sum_{x\in X} v_x(g) \cdot [x]$, where $v_x(g)$ denotes the order of vanishing of $g$ at $x$ and $[x]$ denotes the corresponding point of $X$. Note that $v_x(g)$ is zero for all but finitely many points of $X$, since $g$ is nonzero. Also note that $v_x(g)$ is equal to $n$ if $x\in D$ and $v_x(f)$ if $x\not\in D$. Therefore, $(g)$ is linearly equivalent to the divisor $(f^{n-v_x(g)})$.

Let $h$ be another nonzero function on $D$, represented by a nonzero element $b$ of $A$ and a unit $v$ of $A$. We have $h=bv/f^m$ for some integer $m\geq 0$. The ratio $g/h$ is then equal to $u(v/b)(f^{m-n})$, which is a unit of $A$ (since $A$ is a UFD). Therefore, $(g)$ and $(h)$ are linearly equivalent as divisors on $X$. This shows that every Weil divisor on $X$ is linearly equivalent to a principal divisor, so $Cl(X)$ is trivial. Since $Pic(X)$ is isomorphic to $Cl(X)$ (as explained, for example, in Hartshorne’s Algebraic Geometry, Chapter II, Section 6), we conclude that $Pic(X)$ is also trivial.

问题 2.

(b) Let $X \subset \mathbb{P}^n$ be a projective variety. Suppose that the homogeneous coordinate ring of $X$ is a UFD. Show that $\operatorname{Pic}(X) \cong \mathbb{Z}$.

证明 .

Since $X$ is a projective variety, it is a closed subset of $\mathbb{P}^n$ for some $n$, and hence we may assume that $X$ is a closed subset of $\mathbb{P}^n$ for some $n$. Let $S(X)$ be the homogeneous coordinate ring of $X$, which is a graded ring.

Since $S(X)$ is a UFD, every irreducible homogeneous element of $S(X)$ is a prime element. In particular, every irreducible hypersurface in $\mathbb{P}^n$ that intersects $X$ is a prime divisor on $X$.

Conversely, every prime divisor $D$ on $X$ corresponds to an irreducible hypersurface in $\mathbb{P}^n$ that intersects $X$. By the projective Nullstellensatz, the homogeneous ideal of this hypersurface is generated by homogeneous polynomials of the same degree, and we may assume that these polynomials are irreducible. Since $S(X)$ is a UFD, the irreducible polynomials generate a prime ideal, and hence $D$ is an irreducible element of $\operatorname{Pic}(X)$.

Thus, we have established a bijection between the prime divisors on $X$ and the irreducible elements of $\operatorname{Pic}(X)$. Moreover, every non-zero element of $\operatorname{Pic}(X)$ can be written as a product of irreducible elements, since $S(X)$ is a UFD.

Therefore, $\operatorname{Pic}(X)$ is isomorphic to the group of divisors modulo principal divisors, which is generated by the class of any prime divisor on $X$. Since $X$ is irreducible, any non-empty open subset of $X$ is dense in $X$, and hence any non-zero regular function on $X$ is a unit in $S(X)$. It follows that the group of principal divisors on $X$ is isomorphic to $\mathbb{Z}$, and hence $\operatorname{Pic}(X) \cong \mathbb{Z}$.

问题 3.

Let $X$ be the line with a double point at zero, thus we have a map $X \rightarrow \mathbb{A}^1$ which is an isomorphism over $\mathbb{A}^1 \backslash{0}$ and the preimage of 0 consists of two points.
(a) Let $Y=\mathbb{A}^2 \backslash{0}$. Show that the map $m: Y \rightarrow \mathbb{A}^1, m(x, y)=x y$ can be lifted to an onto map $Y \rightarrow X$; moreover, there are two distinct such liftings.

证明 .

To construct a lifting, we need to find a map $f: Y \rightarrow X$ such that $m = \pi \circ f$, where $\pi: X \rightarrow \mathbb{A}^1$ is the given projection map. Since $m(x,y) = xy$ and $\pi$ has a double point at zero, it’s natural to define $f$ as follows:

  • For $(x,y) \in Y$ with $xy \neq 0$, let $f(x,y) = (x,y)$, i.e., we map $(x,y)$ to itself.
  • For $(x,y) \in Y$ with $xy = 0$, let $f(x,y) = (x,0)$ if $y=0$, and $f(x,y) = (0,y)$ if $x=0$.

It’s clear that $f$ is well-defined and continuous on $Y$. Moreover, since $f(x,y) = (x,y)$ for $(x,y) \in Y \cap (\mathbb{A}^1 \times \mathbb{A}^1)$, where $\mathbb{A}^1 \times \mathbb{A}^1$ is the open subset of $Y$ where both coordinates are nonzero, we have $\pi \circ f = m$ on this open subset. Therefore, $\pi \circ f = m$ on all of $Y$, since both $m$ and $\pi \circ f$ are continuous.

To show that there are two distinct liftings, note that we can also define $f’: Y \rightarrow X$ by interchanging the two coordinates in the second case above:

  • For $(x,y) \in Y$ with $xy \neq 0$, let $f'(x,y) = (x,y)$, i.e., we map $(x,y)$ to itself.
  • For $(x,y) \in Y$ with $xy = 0$, let $f'(x,y) = (0,y)$ if $x=0$, and $f'(x,y) = (x,0)$ if $y=0$.

Then $f’$ is also well-defined and continuous on $Y$, and satisfies $\pi \circ f’ = m$. However, $f$ and $f’$ are not equal, since $f(1,0) = (1,0)$ and $f'(1,0) = (0,0)$. Therefore, we have found two distinct liftings of $m$ to $X$.

这是一份2023年的斯坦福大学Stanford University MATH 145代数几何学写的成功案例




















拓扑学和几何学代写Introduction to Topology and Geometry|MATH 144 Stanford University Assignment

0
Posted on by

Assignment-daixieTM为您提供斯坦福大学Stanford University MATH 144 ntroduction to Topology and Geometry拓扑学和几何学代写代考和辅导服务！

Instructions:

Topology and geometry are two branches of mathematics that deal with the study of shapes and spaces. While they share some similarities, they also have important differences.

Topology is the branch of mathematics concerned with the properties of space that are preserved under continuous transformations, such as stretching or bending. In topology, the focus is on the study of the properties of space that are independent of the exact shape or size of the space. For example, a circle and a square may look very different, but they share important topological properties, such as being closed curves without endpoints.

Geometry, on the other hand, is the branch of mathematics concerned with the study of shape, size, and position of objects in space. Unlike topology, geometry is concerned with the exact properties of space, such as angles, distances, and shapes. Geometry is traditionally divided into two main branches: plane geometry, which deals with objects in two-dimensional space, and solid geometry, which deals with objects in three-dimensional space.

While topology and geometry have different focuses, they are closely related. Many geometric properties can be studied using topological methods, and topology can provide a useful framework for understanding the underlying structure of geometric objects. As a result, topology and geometry often intersect and overlap in interesting and useful ways.

拓扑学和几何学代写Introduction to Topology and Geometry|MATH 144 Stanford University Assignment

问题 1.

(a) Let $[n]$ denote the totally ordered set $\{0,1, \ldots, n\}$. Let $\phi:[m] \rightarrow[n]$ be an order preserving function (so that if $i \leq j$ then $\phi(i) \leq \phi(j)$ ). Identifying the elements of $[n]$ with the vertices of the standard simplex $\Delta^n, \phi$ extends to an affine map $\Delta^m \rightarrow \Delta^n$ that we also denote by $\phi$. Give a formula for this map in terms of barycentric coordinates: If $\phi\left(s_0, \ldots, s_m\right)=\left(t_0, \ldots, t_n\right)$, what is $t_j$ as a function of $\left(s_0, \ldots, s_m\right) ?$

证明 .

We can express the vertices of the standard simplex $\Delta^n$ as the barycentric coordinates $(0,0,\ldots,0,1)$, $(0,0,\ldots,1,0)$, $(0,0,\ldots,1)$, $(0,0,\ldots,1,1,0)$, $(0,0,\ldots,1,0,1)$, $\ldots$, $(1,0,\ldots,0,0)$, $(0,1,\ldots,0,0)$, $(0,0,\ldots,0,1)$, where the $1$ appears in the $i$-th position.

Let $\phi:[m] \rightarrow[n]$ be an order-preserving function, and suppose that $\phi(s_i) = t_j$. Then the affine map $\phi:\Delta^m \rightarrow \Delta^n$ sends the barycentric coordinate $(s_0,\ldots,s_m)$ to the point in $\Delta^n$ whose barycentric coordinates are $(t_0,\ldots,t_n)$.

To compute $t_j$, we note that the $j$-th coordinate of the barycentric coordinates of a point in $\Delta^n$ is given by the sum of the weights of the vertices of $\Delta^n$ that lie in the $j$-th face of $\Delta^n$. In other words, $t_j$ is the sum of the weights of the vertices of $\Delta^n$ whose $j$-th coordinate is $1$.

Let $I_j$ denote the set of indices $i$ such that $\phi(s_i) = j$. Then we have \begin{align*} t_j &= \sum_{i \in I_j} w_i \ &= \sum_{i \in I_j} \prod_{k \neq i} \frac{s_k}{s_k – s_i}, \end{align*} where $w_i$ denotes the weight of the vertex of $\Delta^m$ whose $i$-th coordinate is $1$. The second equality follows from the formula for barycentric coordinates of a point in the simplex.

问题 2.

(b) Write $d^j:[n-1] \rightarrow[n]$ for the order preserving injection that omits $j$ as a value. Show that an order preserving injection $\phi:[n-k] \rightarrow[n]$ is uniquely a composition of the form $d^{j_k} d^{j_{k-1}} \cdots d^{j_1}$, with $0 \leq j_1<j_2<\cdots<j_k \leq n$. Do this by describing the integers $j_1, \ldots, j_k$ directly in terms of $\phi$, and then verify the straightening rule
$$
d^i d^j=d^{j+1} d^i \quad \text { for } \quad i \leq j
$$

证明 .

To describe the integers $j_1,\ldots,j_k$ directly in terms of $\phi$, we proceed by induction on $k$. For $k=1$, we let $j_1$ be the unique value $j$ such that $\phi$ maps $[j-1]$ bijectively onto $\phi([j-1])$ and maps $j$ to $\phi([j-1])\cup{\phi(j)}$. This value exists because $\phi$ is order preserving, so it maps each element of $[n-k]$ to an interval contained in $[n]$, and hence maps $n-k$ to an interval contained in $[n-1]$. By the induction hypothesis, we may assume that $\phi=d^{j_1}\circ\cdots\circ d^{j_{k-1}}\circ d^{j_k’}$ for some integers $j_1<\cdots<j_{k-1}<j_k’\leq n-1$. Let $j_k$ be the unique value such that $\phi$ maps $[j_k-1]$ bijectively onto $\phi([j_k-1])$ and maps $j_k$ to $\phi([j_k-1])\cup{\phi(j_k’)}$. Again, this value exists because $\phi$ is order preserving and maps $j_k’$ to an interval contained in $[n]$. By construction, we have $j_k’>j_{k-1}$, so $j_k$ is strictly greater than all the integers $j_1,\ldots,j_{k-1}$.

We now prove the straightening rule by induction on $i$. For the base case $i=0$, note that $d^0$ is the identity map and hence commutes with $d^j$ for any $j$. For the induction step, suppose that $i\geq 1$ and let $\phi=d^{j_k}\circ\cdots\circ d^{j_1}$ and $\psi=d^i\circ d^j$, where $0\leq j\leq i\leq n-1$. We need to show that $\psi$ can be expressed in the form $d^{j_k’}\circ\cdots\circ d^{j_1′}\circ d^{j_{k+1}’}\circ d^{j_k}\circ\cdots\circ d^{j_{i+1}}$, where $j_1′,\ldots,j_{k+1}’$ are integers such that $0\leq j_1′<\cdots<j_{k+1}’\leq n$. We consider two cases.

Case 1: $j<i\leq j+1$. In this case, we have $\psi=d^i\circ d^j=d^{j+1}\circ d^i$, so we can take $j_1′,\ldots,j_{k+1}’$ to be the same as $j_1,\ldots,j_k,j+1,i$ in some order.

Case 2: $i\leq j$. In this case, we have $\psi=d^i\circ d^j=d^{j}\circ d^{i+1}$, so by the induction hypothesis, we can write $\phi$ in the form $d^{j_k’}\circ\cdots\circ d^{j_1′}\circ d^{j_k}\circ\cdots\circ d^{j_{i+1}}$ for some integers $j_1′<\cdots<j_k’\leq n-1

问题 3.

(c) Show that any order preserving map $\phi:[m] \rightarrow[n]$ factors uniquely as the composition of an order preserving surjection followed by an order preserving injection

证明 .

Let $\phi:[m]\rightarrow [n]$ be an order preserving map. We will first show that $\phi$ factors as the composition of an order preserving surjection followed by an order preserving injection. Then, we will show that this factorization is unique.

Let $X = {i \in [m] \mid \phi(i) = \min_{j\in [m]} \phi(j)}$ be the set of elements of $[m]$ that are mapped to the smallest element in the range of $\phi$. Since $\phi$ is order preserving, $X$ is non-empty and has a smallest element $x_0$. Define $Y = {\phi(x) \mid x\in [m], \phi(x) \geq \phi(x_0)}$. Note that $Y$ is a subset of $[n]$ and is non-empty since it contains $\phi(x_0)$. We claim that the map $\psi:[m]\rightarrow Y$ defined by $\psi(x) = \phi(x)$ for $x\in X$ and $\psi(x) = \min{\phi(y) \mid y>x, \phi(y) \in Y}$ for $x\notin X$ is an order preserving surjection.

To see that $\psi$ is order preserving, let $x,y\in[m]$ be such that $x\leq y$. If $\phi(x) = \phi(y)$, then it follows immediately that $\psi(x) = \psi(y)$. Otherwise, we have $\phi(x) < \phi(y)$. Since $\phi$ is order preserving, we also have $\psi(x) \leq \phi(x) < \phi(y) \leq \psi(y)$. Thus, $\psi$ is order preserving.

To see that $\psi$ is surjective, let $y\in Y$. If $y = \phi(x_0)$, then $x_0\in X$ and $\psi(x_0) = y$. Otherwise, let $x\in[m]$ be such that $\phi(x) = y$. Since $y\in Y$, we have $\phi(x) \geq \phi(x_0)$, so $x\notin X$. Since $\phi$ is order preserving, there exists $z>x$ such that $\phi(z) = \min{\phi(w) \mid w>x, \phi(w) \in Y}$. Since $y\in Y$, we have $\phi(z) \in Y$, so $\psi(z) \leq \phi(z)$. But $\psi(x) = \min{\phi(w) \mid w>x, \phi(w) \in Y}$ by definition of $\psi$, so we must have $\psi(z) > \psi(x)$. Therefore, there exists $w\in[m]$ such that $\psi(w) = y$, so $\psi$ is surjective.

To see that $\psi$ is a surjection, let $y_1,y_2\in Y$ be such that $y_1 < y_2$. Then there exist $x_1,x_2\in [m]$ such that $\phi(x_1) = y_1$ and $\phi(x_2) = y_2$. Since $\phi$ is order preserving and $y_1 < y_2$, we have $x_1 < x_2$. Therefore, $\psi(x_1) = y_1$ and $\psi(x_2) \geq y_2$, so $\psi$ is a surjection.

这是一份2023年的斯坦福大学Stanford University MATH 143微分几何学写的成功案例




















数论 Number Theory II|MATH 8822Boston College Assignment

0
Posted on by

Assignment-daixieTM为您提供波士顿学院Boston College MATH 8822 Number Theory II数论代写代考和辅导服务！






Instructions:





Factorization of Ideals: The factorization of ideals in algebraic number theory is an extension of prime factorization in the integers. Given an algebraic number field K, we can define an ideal I to be a subset of K consisting of elements that are divisible by a fixed non-zero element of K. The factorization of an ideal into a product of prime ideals is unique up to order and multiplication by units of the ring of integers of K. This factorization has important applications in algebraic number theory, including the proof of Fermat’s Last Theorem.





Local Fields: A local field is a field that is complete with respect to a non-archimedean absolute value. Examples of local fields include p-adic numbers and function fields over a finite field. Local fields have important applications in number theory, representation theory, and algebraic geometry.















数论 Number Theory II|MATH 8822Boston College Assignment













问题 1. 





Let $(L, \leq)$ be a partially ordered set in which every countable chain has an upper bound. Let $S \subseteq L$ be countable such that for all $a, b \in S$ there is $c \in S$ such that $a \leq c$ and $b \leq c$. Prove that $S$ has an upper bound in $L$.





 
 




证明 . 





To prove that $S$ has an upper bound in $L$, we will use Zorn’s lemma. Let $T$ be the set of all chains in $L$ that are contained in $S$, and let $C$ be a chain in $T$. We want to show that $C$ has an upper bound in $L$.





Since $C$ is a chain in $L$, we know that $(C, \leq)$ is a partially ordered set. Let $c$ be an upper bound for $C$ in $L$. We claim that $c$ is also an upper bound for $S$.





Suppose for the sake of contradiction that $c$ is not an upper bound for $S$. Then there exists some $s \in S$ such that $s \nleq c$. Since $S \subseteq C$, we know that $s \in C$. Since $c$ is an upper bound for $C$, we have $s \leq c$. This contradicts the assumption that $s \nleq c$, so our claim is proven.





Therefore, $c$ is an upper bound for $S$. To complete the proof, we need to show that $c$ is in fact an element of $L$. Since every countable chain in $L$ has an upper bound, we know that $L$ is a complete partial order. In particular, every chain in $L$ has a least upper bound (lub).





Let $D$ be the set of all upper bounds of $S$ in $L$. We want to show that $c = \operatorname{lub}(D)$, which will complete the proof. First, we show that $c$ is an upper bound of $S$. We have already shown this above.





Now, let $d$ be an upper bound of $S$ in $L$. We want to show that $c \leq d$. By definition of $D$, we have $c \in D$, so $c$ is an upper bound of $S$. Therefore, we have $c \leq d$, since $d$ is also an upper bound of $S$.





Finally, we need to show that $c$ is the least upper bound of $D$. Suppose for the sake of contradiction that there exists some $d’ \in L$ such that $d’ < c$ and $d’$ is an upper bound of $D$. Since $c$ is an upper bound of $D$, we have $d’ \leq c$. But this contradicts the assumption that $c$ is the least upper bound of $D$. Therefore, $c$ must be the least upper bound of $D$.





We have now shown that $S$ has an upper bound in $L$. Therefore, by definition of a complete partial order, $L$ has a least upper bound for $S$, which completes the proof.














问题 2. Prove that for all nonnegative integers $n \geq 0$ and $k>1, \sqrt[k]{n}$ is rational if and only if $n=d^k$ for some integer $d$.





 
 




证明 . 





First, let’s assume that $\sqrt[k]{n}$ is rational. This means that there exists some integers $a$ and $b$ such that $\sqrt[k]{n}=\frac{a}{b}$, where $b\neq 0$. Raising both sides to the $k$-th power gives us $n=\frac{a^k}{b^k}$, which can be written as $nb^k=a^k$. This shows that $a^k$ is a multiple of $b^k$, which implies that $a$ must be a multiple of $b$. Let $a=cb$ for some integer $c$. Then we have $n=cb^k$, which can be written as $n=(b^{k-1}c)^k$. Therefore, $n$ is of the form $d^k$ for some integer $d=b^{k-1}c$.





Now let’s assume that $n=d^k$ for some integer $d$. We can write $d$ as $d=be$, where $b$ is the largest integer such that $b^k$ divides $d^k$, and $e$ is some integer. Then $n=d^k=(be)^k=b^ke^k$. Since $b$ is the largest integer such that $b^k$ divides $d^k$, $e$ is not divisible by $b$. Therefore, $b$ and $e$ are relatively prime. This implies that $b^k$ and $e^k$ are also relatively prime. Thus, $n=b^ke^k$ is in its simplest form as a product of relatively prime integers, and its $k$-th root is $\sqrt[k]{n}=e\in \mathbb{Z}$. Therefore, $\sqrt[k]{n}$ is rational.





Combining the two directions of the proof, we have shown that for all nonnegative integers $n \geq 0$ and $k>1$, $\sqrt[k]{n}$ is rational if and only if $n=d^k$ for some integer $d$.










问题 3. 





Suppose $p, q, r$ are integers such that $\sqrt{p}+\sqrt{q}+\sqrt{r}=s \in \mathbb{Q}$. Prove that $p, q, r$ are perfect squares.





 
 




证明 . 





Let $s=\sqrt{p}+\sqrt{q}+\sqrt{r}$.





Squaring both sides, we get:





$$s^2=p+q+r+2\sqrt{pq}+2\sqrt{qr}+2\sqrt{rp}$$





Since $s$ is rational, $s^2$ is also rational. Thus, $\sqrt{pq}$, $\sqrt{qr}$, and $\sqrt{rp}$ must be rational.





Suppose, for contradiction, that $p$ is not a perfect square. Then, $\sqrt{p}$ is irrational, and $\sqrt{q}+\sqrt{r}=s-\sqrt{p}$ is also irrational.





But this implies that $\sqrt{pq}$ and $\sqrt{qr}$ are irrational, which contradicts the fact that they are rational. Thus, $p$ must be a perfect square.





Similarly, we can show that $q$ and $r$ are also perfect squares. Thus, $p$, $q$, and $r$ are all perfect squares, as required.
























这是一份2023年的波士顿学院Boston College MATH 8822数论代写的成功案例




























































































































































			

	
	



		
			


	

		
物理统计学 Statistical Physics II|PHYS7722 Boston College Assignment


				0
		
				

			Posted on  by 		

		
	


		

		

Assignment-daixieTM为您提供波士顿学院Boston College PHYS7722 Statistical Physics II物理统计学代写代考和辅导服务！










Instructions:





Statistical physics is a branch of physics that studies the behavior of large collections of particles, such as atoms or molecules, using statistical methods. It aims to explain macroscopic properties of matter, such as temperature, pressure, and entropy, in terms of the microscopic properties of the constituent particles and the interactions between them.





Statistical physics is based on the principles of probability and statistics, and it provides a framework for understanding complex systems that cannot be analyzed through classical physics. It also provides a link between the microscopic world of quantum mechanics and the macroscopic world of classical mechanics.















物理统计学 Statistical Physics II|PHYS7722 Boston College Assignment













问题 1. 





The partition function for an ideal gas of $N$ distinguishable particles where particle $k$ has mass $m_k$ can be written as
$$
Z=\frac{1}{h^{3 N}} \int_V d^3 \mathbf{q}1 \int{\text {all } \mathbf{p}} d^3 \mathbf{p}1 \cdots \int_V d^3 \mathbf{q}_N \int{\text {all } \mathbf{p}} d^3 \mathbf{p}N \exp \left(-\frac{1}{k_B T} \sum{k=1}^N \frac{\mathbf{p}_k^2}{2 m_k}\right) .,
$$
where $V$ is the volume of the system.
(a)  Evaluate all the integrals in Eq.(40) and write the final result in terms of $T, V, N$ and the set of masses $m_1, m_2, \ldots, m_N$ (and physical constants).





 
 




证明 . 





We can evaluate the integrals by using the fact that they represent the phase space integral for each particle. The integral $\int{d^3\mathbf{q}_k} \int{\text{all } \mathbf{p}_k}d^3\mathbf{p}_k$ represents the phase space integral for the $k$th particle. We can perform this integral by changing to spherical coordinates for the momentum integral and making use of the fact that the volume element $d^3 \mathbf{p}$ is $4\pi p^2dp$, where $p$ is the magnitude of the momentum vector. Thus, we have





$\int d^3 \mathbf{q}_k \int$ all $\mathbf{p}_k d^3 \mathbf{p}_k=V \int_0^{\infty} 4 \pi p_k^2 d p_k=\frac{4}{3} \pi V\left(\frac{2 \pi m_k k_B T}{h^2}\right)^{3 / 2}$





Using this result, we can evaluate the integral over all particles in the partition function: \begin{align*} Z &= \frac{1}{h^{3N}} \prod_{k=1}^N \int{d^3\mathbf{q}_k} \int{\text{all } \mathbf{p}k}d^3\mathbf{p}k \exp \left(-\frac{1}{k_B T} \sum{k=1}^N \frac{\mathbf{p}k^2}{2m_k}\right)\ &= \frac{1}{h^{3N}} \prod{k=1}^N \frac{4}{3} \pi V \left(\frac{2\pi m_k k_B T}{h^2}\right)^{3/2} \exp \left(-\frac{1}{k_B T} \frac{\mathbf{p}k^2}{2m_k}\right)\ &= \frac{1}{N! h^{3N}} V^N \prod{k=1}^N \left(\frac{2\pi m_k k_B T}{h^2}\right)^{3/2} \exp \left(-\frac{1}{k_B T} \frac{\mathbf{p}k^2}{2m_k}\right)\ &= \frac{1}{N!} \left(\frac{V}{v_N}\right)^N \prod{k=1}^N \left(\frac{mk_B T}{2\pi\hbar^2}\right)^{3/2}, \end{align*} where $v_N$ is the volume occupied by a single particle, defined by $v_N = \frac{4}{3}\pi\left(\frac{\hbar}{\sqrt{2\pi mk_B T}}\right)^3$ and $m$ is the average mass of a particle, defined by $m = \frac{1}{N}\sum{k=1}^N m_k$. The result is written in terms of physical constants and the set of masses $m_1, m_2, \ldots, m_N$.






















问题 2. What is the free energy of this system written in terms of $T, V, N$ and the set of masses $m_1, m_2, \ldots, m_N$ (and physical constants).





 
 




证明 . 





(b) Given the partition function $Z$ of a system, the free energy is
$$
F=-k_B T \ln Z
$$
Therefore, the free energy of this ideal gas system is
$$
\begin{aligned}
F & =-k_B T \ln \left[\frac{V^N}{h^{3 N}}\left(2 \pi k_B T\right)^{3 N / 2} \prod_{k=1}^N \sqrt{m_k^3}\right] \
& =-k_B T \ln \left[V^N\left(\frac{2 \pi k_B T}{h^2}\right)^{3 N / 2} \prod_{k=1}^N m_k^{3 / 2}\right] \
& =-k_B T\left[N \ln V+\frac{3 N}{2} \ln \frac{2 \pi k_B T}{h^2}+\frac{3}{2} \sum_{k=1}^N \ln m_k\right] .
\end{aligned}
$$










问题 3. 





(c) Given that pressure is the negative of the volume partial derivative of the free energy, derive the relationship between pressure $P$, number of particles $N$, volume $V$ and temperature $T$ for this system.





 
 




证明 . 





(c) The pressure of an ideal gas system is given by
$$
P=-\frac{\partial F}{\partial V}
$$
Computing the pressure from Eq.(45), we find
$\begin{aligned} P & =-\frac{\partial}{\partial V}\left{-k_B T\left[N \ln V+\frac{3 N}{2} \ln \frac{2 \pi k_B T}{h^2}+\frac{3}{2} \sum_{k=1}^N \ln m_k\right]\right} \ & =k_B T \frac{\partial}{\partial V} N \ln V=k_B T N \frac{1}{V},\end{aligned}$
where in the second line we dropped all terms which were independent of $V$. Therefore, we have
$$
P=\frac{N k_B T}{V}
$$
which is the standard ideal gas law for identical particles. Therefore, we see that the ideal gas law does not change when the particles are not identical.




















这是一份2023年的波士顿学院Boston College PHYS7722 物理统计学代写的成功案例




























































































































































			

	
	



		
			


	

		
统计物理学 Statistical Physics I|PHYS7721Boston College Assignment


				0
		
				

			Posted on  by 		

		
	


		

		

Assignment-daixieTM为您提供波士顿学院Boston College PHYS7721  Statistical Physics I 统计物理学代写代考和辅导服务！










Instructions:





Statistical physics is a branch of physics that uses statistical methods to explain the behavior of systems made up of many interacting particles. It seeks to understand the collective behavior of these particles in terms of the laws of physics and probability theory.





In statistical physics, the properties of a macroscopic system, such as temperature, pressure, and entropy, are derived from the statistical properties of the individual particles that make up the system. This approach is based on the assumption that the particles are in thermal equilibrium and that their interactions can be treated statistically.





One of the central concepts in statistical physics is the partition function, which is used to calculate the thermodynamic properties of a system. The partition function is a sum over all possible states of the system, weighted by their probability.





Statistical physics has many applications in fields such as condensed matter physics, astrophysics, and biophysics. It is also used in the study of phase transitions, critical phenomena, and the behavior of complex systems.















统计物理学 Statistical Physics I|PHYS7721Boston College Assignment













问题 1. 





For a particular model of a gene in a cell, the probability density that said gene produces a concentration $x$ of proteins during the cell cycle is given by
$$
p(x)=A\left(\frac{x}{b}\right)^N e^{-x / b},
$$
where $b$ is a biological constant with units of concentration, $N$ is a physical constant, and $A$ is a normalization parameter.
(a) The concentration of proteins that can be produced ranges from zero to infinite. What must $A$ be in order for Eq.(1) to be normalized?





 
 




证明 . 





(a) Given the range of possible protein production, $x$ can go from 0 to $\infty$. Therefore, for $p(x)$ to be normalized, we must obtain 1 when we integrate the function over this entire domain:
$$
\int_0^{\infty} d x p(x)=1 .
$$
From the definition of the probability density we have
$$
\begin{aligned}
1 & =\int_0^{\infty} d x A\left(\frac{x}{b}\right)^N e^{-x / b} \
& =A \int_0^{\infty} d x\left(\frac{x}{b}\right)^N e^{-x / b} \
& =A \int_0^{\infty} d u b u^N e^{-u} \
& =A b \int_0^{\infty} d u u^N e^{-u},
\end{aligned}
$$
where we changed variables with $u=x / b$ in the third line, and factored the $u$-independent constant out of the integral in the final line. By the integral definition of factorial, we have
$$
N !=\int_0^{\infty} d u u^N e^{-u} .
$$
Therefore, the final line of Eq.(4) becomes
$$
1=A b N !,
$$
and we can conclude
$$
A=\frac{1}{b N !} .
$$





The normalized probability density is therefore
$$
p(x)=\frac{1}{b N !}\left(\frac{x}{b}\right)^N e^{-x / b} .
$$














问题 2. (b)What is the mean of the normalized probability density?





 
 




证明 . 





(b) The mean of a random variable defined by the probability density $p(x)$ (which has a nonzero domain for $x \in[0, \infty)$ ) is
$$
\langle x\rangle=\int_0^{\infty} d x \operatorname{xp}(x) .
$$
Using Eq.(8) to compute this value, we obtain
$$
\begin{aligned}
\langle x\rangle & =\int_0^{\infty} d x x \frac{1}{b N !}\left(\frac{x}{b}\right)^N e^{-x / b} \
& =\frac{1}{N !} \int_0^{\infty} d x\left(\frac{x}{b}\right)^{N+1} e^{-x / b} \
& =\frac{1}{N !} \int_0^{\infty} d u b u^{N+1} e^{-u} \
& =b \frac{(N+1) !}{N !}
\end{aligned}
$$
where in the third line we performed a change of variables with $u=x / b$ and in the final line we used Eq. By the definition of factorial, we ultimately find
$$
\langle x\rangle=b(N+1)
$$










问题 3. 





(c) For this probability distribution, compute the average
$$
\left\langle e^{x / a}\right\rangle,
$$
and write the result in terms of an infinite sum over a binomial coefficient. (Note that $e^x=$ $\sum_{j=0}^{\infty} x^j / j !$.)





 
 




证明 . 





(c) We now seek to compute the average of $e^{x / a}$. Noting the Taylor series definition of the exponential
$$
e^{x / a}=\sum_{j=0}^{\infty} \frac{(x / a)^j}{j !},
$$
we have
$$
\begin{aligned}
\left\langle e^{x / a}\right\rangle & =\left\langle\sum_{j=0}^{\infty} \frac{(x / a)^j}{j !}\right\rangle \
& =\sum_{j=0}^{\infty} \frac{1}{j !} \frac{1}{a^j}\left\langle x^j\right\rangle .
\end{aligned}
$$
Computing $\left\langle x^j\right\rangle$ yields
$$
\begin{aligned}
\left\langle x^j\right\rangle & =\int_0^{\infty} d x x^j \frac{1}{b N !}\left(\frac{x}{b}\right)^N e^{-x / b} \
& =\frac{b^j}{b N !} \int_0^{\infty} d x\left(\frac{x}{b}\right)^{N+j} e^{-x / b} \
& =\frac{b^j}{b N !} \int_0^{\infty} d u b u^{N+j} e^{-u}
\end{aligned}
$$





$$
=b^j \frac{(N+j) !}{N !}
$$
where in the second line we multiplied the numerator and the denominator by $b^j$, in the third line we performed a change of variables $u=x / b$, and in the final line we used Eq.(5). Inserting this result into Eq.(13), we find
$$
\left\langle e^{x / a}\right\rangle=\sum \sum_{j=0}^{\infty} \frac{1}{j !} \frac{1}{a^j} b^j \frac{(N+j) !}{N !}=\sum_{j=0}^{\infty} \frac{(N+j) !}{j ! N !}\left(\frac{b}{a}\right)^j,
$$
or
$$
\left\langle e^{x / a}\right\rangle=\sum_{j=0}^{\infty}\left(\begin{array}{c}
N+j \
j
\end{array}\right)\left(\frac{b}{a}\right)^j
$$
We note that we could evaluate $\left\langle e^{x / a}\right\rangle$ directly using a change of variables in the argument of the exponential of the distribution. The result would be
$$
\begin{aligned}
\left\langle e^{x / a}\right\rangle & =\frac{1}{b N !} \int_0^{\infty} d x e^{x / a}\left(\frac{x}{b}\right)^N e^{-x / b} \
& =\frac{1}{b N !} \int_0^{\infty} d x\left(\frac{x}{b}\right)^N e^{-(1 / b-1 / a) x} \
& =\frac{1}{b N !} \int_0^{\infty} d u \frac{a b}{a-b}\left(\frac{a u}{a-b}\right)^N e^{-u} \
& =\frac{1}{N !}\left(\frac{a}{a-b}\right)^{N+1} \int_0^{\infty} d u u^N e^{-u} \
& =\frac{1}{(1-b / a)^{N+1}},
\end{aligned}
$$
where in the second line we made the change of variables $u=x(a-b) / a b$. Considering Eq.(16), the result Eq.(17) implies
$$
\sum_{j=0}^{\infty}\left(\begin{array}{c}
N+j \
j
\end{array}\right) q^j=\frac{1}{(1-q)^{N+1}}
$$




















这是一份2023年的波士顿学院Boston College PHYS7721统计物理学代写的成功案例




























































































































































			

	
	



		
			


	

		
经典力学 Classical Mechanics|PHYS7711Boston College Assignment


				0
		
				

			Posted on  by 		

		
	


		

		

Assignment-daixieTM为您提供波士顿学院Boston College PHYS7711 Classical Mechanics 经典力学代写代考和辅导服务！










Instructions:





Classical mechanics is a branch of physics that deals with the motion of objects under the influence of forces. It provides a framework for describing and predicting the behavior of physical systems ranging from the motion of planets and satellites to the behavior of atoms and molecules.





Classical mechanics is based on three fundamental laws of motion, known as Newton’s laws. The first law states that an object at rest will remain at rest, and an object in motion will continue to move in a straight line with constant velocity, unless acted upon by an external force. The second law relates the force acting on an object to its acceleration: F = ma, where F is the force, m is the mass of the object, and a is its acceleration. The third law states that for every action, there is an equal and opposite reaction.





In addition to these laws, classical mechanics also includes the concept of energy, both kinetic and potential. Kinetic energy is the energy possessed by an object due to its motion, while potential energy is the energy associated with the position or configuration of an object.





Classical mechanics is essential for understanding many areas of science and technology, including astronomy, engineering, and mechanics. It forms the foundation for many other branches of physics, such as thermodynamics, electromagnetism, and quantum mechanics.















经典力学 Classical Mechanics|PHYS7711Boston College Assignment













问题 1. 





Consider the motion of an object close to the surface of the Earth moving under the influence of Earth’s gravity.
a) The gravitational force law
$$
\vec{F}=-\frac{G M m}{r^2} \hat{r}
$$
reduces to
$$
\vec{F}=-g m \hat{z}
$$
at the surface with $z$ pointing away from the center of the Earth (i.e., “up”). Express $g$ in terms of $G$, $M_{\oplus}$ and $R_{\oplus}$. Compute $g$ in SI units.





 
 




证明 . 





At the surface of the Earth, the distance $r$ from the center of the Earth to the object is equal to the radius of the Earth, $R_{\oplus}$. Thus, we have





$\vec{F}=-\frac{G M_{\oplus} m}{R_{\oplus}^2} \hat{r} \approx-\frac{G M_{\oplus} m}{R_{\oplus}^2} \hat{z}$





where we have approximated $\hat{r}$ by $\hat{z}$ because the surface of the Earth is approximately a plane perpendicular to the $z$-axis.





The magnitude of the force is given by





$F=|\vec{F}|=\frac{G M_{\oplus} m}{R_{\oplus}^2}$





By Newton’s second law, the force is related to the object’s mass $m$ and acceleration $a$ via





$\vec{F}=m \vec{a}$





Since the object is moving only vertically, we have $\vec{a}=a\hat{z}$ and $|\vec{a}|=a$. Therefore,





F=ma=mg





where $g=|\vec{a}|$ is the acceleration due to gravity. Combining these equations, we obtain









$m g=\frac{G M_{\oplus} m}{R_{\oplus}^2}$





which can be solved for $g$ to give





$g=\frac{G M_{\oplus}}{R_{\oplus}^2}$





Substituting the values for $G$, $M_{\oplus}$, and $R_{\oplus}$ in SI units, we have





$g=\frac{\left(6.674 \times 10^{-11} \mathrm{~m}^3 \mathrm{~kg}^{-1} \mathrm{~s}^{-2}\right) \times\left(5.9722 \times 10^{24} \mathrm{~kg}\right)}{\left(6.371 \times 10^6 \mathrm{~m}\right)^2} \approx 9.81 \mathrm{~m} / \mathrm{s}^2$





Therefore, the acceleration due to gravity at the surface of the Earth is approximately $9.81 ,\mathrm{m/s^2}$.






















问题 2. Consider the motion of an object close to the surface of the Earth moving under the influence of Earth’s gravity. b) For a cannonball fired at velocity $v_o$ and angle $\theta$ above the horizon on the Moon, find the range; the distance from the cannon at which the cannonball hits the surface of the Moon. (You will need to recompute $g$ for the Moon, but the lack of air on the Moon makes this calculation much easier there than on Earth.)





 
 




证明 . 





The range, $R$, of a projectile launched at an angle $\theta$ above the horizon with initial velocity $v_0$ is given by:





$$R = \frac{v_0^2\sin(2\theta)}{g},$$





where $g$ is the acceleration due to gravity.





On the Moon, the acceleration due to gravity is $g_{\text{Moon}} = 1.62 \text{ m/s}^2$. Therefore, the range of a cannonball fired at velocity $v_0$ and angle $\theta$ above the horizon on the Moon is:





$$R = \frac{v_0^2\sin(2\theta)}{g_{\text{Moon}}}.$$





Note that since there is no air on the Moon, we do not need to worry about air resistance affecting the motion of the cannonball.










问题 3. 





Hooke’s law for a spring of constant $k$ is $F=-k x$. A mass $m$ is pushed from position $x_o$ with velocity $v_o$ at $t=0$. Find the subsequent motion, $x(t)$.





 
 




证明 . 





The equation of motion for a mass on a spring is given by Newton’s second law: $F = ma$, where $F$ is the force exerted by the spring, $m$ is the mass of the object attached to the spring, and $a$ is its acceleration. In this case, the force exerted by the spring is given by Hooke’s law, $F = -kx$, where $x$ is the displacement of the mass from its equilibrium position.





Assuming that the mass is only moving along the $x$-axis, we can write the equation of motion as:





ma=−kx





Since $a = \frac{d^2x}{dt^2}$, we can rewrite this as:





$m \frac{d^2 x}{d t^2}=-k x$





This is a second-order ordinary differential equation, which we can solve using the characteristic equation method. We assume that the solution takes the form:





$x(t)=A \cos (\omega t)+B \sin (\omega t)$





where $A$ and $B$ are constants that depend on the initial conditions, and $\omega$ is the angular frequency of the oscillation. Substituting this into the differential equation, we get:





$-\omega^2 m(A \cos (\omega t)+B \sin (\omega t))=-k(A \cos (\omega t)+B \sin (\omega t))$





Dividing both sides by $A\cos(\omega t) + B\sin(\omega t)$, we get:





$-\omega^2 m=-k \Rightarrow \omega=\sqrt{\frac{k}{m}}$





So the general solution is:





$x(t)=A \cos \left(\sqrt{\frac{k}{m}} t\right)+B \sin \left(\sqrt{\frac{k}{m}} t\right)$





To find the constants $A$ and $B$, we use the initial conditions. At $t=0$, the mass is at position $x_0$ with velocity $v_0$. So we have:





$x(0)=x_0 \Rightarrow A=x_0$





and





$v(0)=\left.\frac{d x}{d t}\right|_{t=0}=v_0=-\sqrt{\frac{k}{m}} x_0+B \sqrt{\frac{k}{m}}$





Solving for $B$, we get:





$B=\frac{v_0+\sqrt{\frac{k}{m}} x_0}{\sqrt{\frac{k}{m}}}$





Therefore, the solution for $x(t)$ is:





$x(t)=x_0 \cos \left(\sqrt{\frac{k}{m}} t\right)+\frac{v_0}{\sqrt{\frac{k}{m}}} \sin \left(\sqrt{\frac{k}{m}} t\right)$





This is the position of the mass as a function of time, given its initial position and velocity.




















这是一份2023年的波士顿学院Boston College PHYS7711 经典力学代写的成功案例




























































































































































			

	
	



		
			


	

		
代数和数论 Topics in Algebra and Number Theory|MATH 8845Boston College Assignment


				0
		
				

			Posted on  by 		

		
	


		

		

Assignment-daixieTM为您提供波士顿学院Boston College MATH 8845 Topics in Algebra and Number Theory代数和数论代写代考和辅导服务！










Instructions:





Algebra is a branch of mathematics that deals with the manipulation and properties of abstract objects, such as numbers, symbols, and equations. It includes the study of algebraic structures, such as groups, rings, and fields, and their properties and applications.





Number theory is a branch of mathematics that deals with the properties of numbers, particularly integers. It includes the study of prime numbers, divisibility, Diophantine equations, and modular arithmetic, among other topics.





Algebra and number theory are closely related, as algebraic structures such as groups, rings, and fields are often used in the study of number theory. For example, the study of prime numbers can be approached using algebraic techniques such as group theory, and the study of modular arithmetic relies heavily on properties of rings and fields. Many problems in number theory also have algebraic formulations and solutions.















代数和数论 Topics in Algebra and Number Theory|MATH 8845Boston College Assignment













问题 1. 





Let $m=3^n p$ for some integer $n>0$ and prime $p$. Suppose $m$ is perfect.
(a) Prove that if $p \neq 2$ then $3^{n+1}-1=2 p$ and $p+1=2 \cdot 3^n$.





 
 




证明 . 





Since $m$ is a perfect number, it must be of the form $m=2^{k-1}(2^k-1)$ for some positive integer $k$. Therefore, we have





$$m = 2^{k-1}(2^k-1) = 3^n p.$$





Since $p$ is prime and $p\neq 2$, we have two cases:





Case 1: $p\equiv 1\pmod 3$





In this case, we have $3^n \mid 2^{k-1}$, which implies $k-1\geq n$. Furthermore, since $p\equiv 1\pmod 3$, we have $p+1\equiv 2\pmod 3$, which implies $3\mid p+1$. Thus, we have





$$m = 2^{k-1}(2^k-1) \geq 2^{n}(2^{n+1}-1) > 2^n(2\cdot 3^n -1) = 2p,$$





which contradicts the fact that $m$ is perfect. Therefore, this case cannot occur.





Case 2: $p\equiv 2\pmod 3$





In this case, we have $3^n \mid 2^k-1$, which implies $k\geq n+1$. Furthermore, since $p\equiv 2\pmod 3$, we have $p+1\equiv 0\pmod 3$, which implies $3^{n+1}\mid p+1$. Thus, we have





$$m = 2^{k-1}(2^k-1) \geq 2^{n}(2^{n+1}-1) = 3^n(3^{n+1}-2) > 3^n(3^n\cdot 2 – 2) = 2\cdot 3^{2n} > 2p,$$





which again contradicts the fact that $m$ is perfect. Therefore, this case cannot occur either.





Therefore, there is no prime $p\neq 2$ that can make $m$ a perfect number.





Note: If $p=2$, then $m=2^{2n+1}-2^n$, and it is known that this is a perfect number if and only if $2^n$ is an odd prime (known as Mersenne prime).














问题 2. Let $m=3^n p$ for some integer $n>0$ and prime $p$. Suppose $m$ is perfect. Prove that $p=2$.





 
 




证明 . 





Since $m$ is perfect, we know that the sum of its divisors (excluding itself) is equal to $m$. That is, if $d_1,d_2,\ldots,d_k$ are the positive divisors of $m$ (excluding $m$ itself), then we have $$d_1+d_2+\cdots+d_k=m.$$ Now let $d$ be any positive divisor of $m$. Then $d$ can be written as $3^ap^b$ for some nonnegative integers $a$ and $b$ with $0\leq b\leq 1$. (Note that $b=0$ is possible because $m$ need not be odd.) Since $d$ divides $m$, we have $3^ap^b\mid 3^n p$, which implies $3^a\mid 3^n$. Therefore, $a\leq n$. It follows that $d\leq 3^n p$.





Now consider the sum of the divisors of $m$ that are divisible by $3$. These are precisely the divisors of the form $3^ap$ with $1\leq a\leq n$. There are $n$ such divisors, each of which is at most $3^n p$, so the sum of these divisors is at most $n\cdot 3^n p$. Therefore, the sum of the divisors of $m$ that are not divisible by $3$ is at least $$m-(n\cdot 3^n p)=(3^n- n\cdot 3^n)p.$$ Since $m$ is perfect, this sum must be equal to $m$. That is, $$(3^n-n\cdot 3^n)p=3^n p+2^k,$$ where $k$ is a nonnegative integer and $2^k$ is the sum of the divisors of $m$ that are equal to $2^j$ for some $j\geq 1$. Since $p$ is prime, it follows that $p$ divides $2^k$. However, $p$ is odd because $p\neq 2$, so $p$ and $2$ are relatively prime. Therefore, we must have $p=2$.










问题 3. 





Let $m=3^n p$ for some integer $n>0$ and prime $p$. Suppose $m$ is perfect. Prove that $m=6$.





 
 




证明 . 





Let $d(m)$ denote the sum of the divisors of $m$. If $m$ is perfect, then $d(m)=2m$.





Since $m=3^n p$, the sum of the divisors of $m$ is given by $(1+3+\cdots+3^n)(1+p)$, which is equal to $\frac{3^{n+1}-1}{2}(p+1)$.





Thus, we have the equation $\frac{3^{n+1}-1}{2}(p+1)=2(3^n p)$.





Rearranging terms, we get $3^{n+1}p-3^n-1=0$.





Now, we observe that if $n\geq 2$, then $3^{n+1}p-3^n-1 \equiv 2 \pmod{3}$, which means that $3^n p$ cannot be perfect. Therefore, we must have $n=1$.





Plugging in $n=1$, we get $3p-2=0$, which implies $p=2/3$, a contradiction since $p$ is prime.





Therefore, there is no such $m$ such that $m=3^n p$ and $m$ is perfect.




















这是一份2023年的波士顿学院Boston College MATH 8845代数和数论代写的成功案例




























































































































































			

	
	



		
			


	

		
几何学/拓扑学代写 Geometry/Topology III |MATH 8831 Boston College Assignment


				0
		
				

			Posted on  by 		

		
	


		

		

Assignment-daixieTM为您提供波士顿学院Boston College MATH 8831 Geometry/Topology III 几何学/拓扑学代写代考和辅导服务！










Instructions:





Differential geometry is a branch of mathematics that deals with the study of geometric objects using techniques from calculus, linear algebra, and topology. It provides a framework for studying curves, surfaces, manifolds, and other geometric structures.





One of the key ideas in differential geometry is the concept of a tangent space. The tangent space at a point on a manifold is the space of all possible velocities or directions that can be taken from that point. This concept is essential for understanding how geometric objects change and interact with each other.





Another important concept in differential geometry is the notion of a connection. A connection is a way of measuring the deviation of a curve or surface from being flat. Connections are used to define important geometric quantities such as curvature, which measures how much a curve or surface deviates from being a straight line or plane.





Differential geometry has numerous applications in physics, engineering, and computer science. For example, it is used in the study of general relativity, which describes the behavior of gravity in the presence of curved spacetime. It is also used in computer graphics and robotics to model and control the motion of objects in three-dimensional space.















几何学/拓扑学代写 Geometry/Topology III |MATH 8831 Boston College Assignment













问题 1. 





Let $(J, \omega)$ be a Kähler structure, and let $\beta$ be a holomorphic Poisson structure, so that $\mathcal{J}_B=e^{t Q} \mathcal{J}_J e^{-t Q}$ is integrable for all $t$. What is the condition on $\beta$ which guarantees that $\mathcal{J}_A=e^{t Q} \mathcal{J}_\omega e^{-t Q}$ is integrable for small $t$ ? What are the resulting types of $\left(\mathcal{J}_A, \mathcal{J}_B\right)$ ?





 
 




证明 . 





The condition that guarantees integrability of $\mathcal{J}A$ for small $t$ is that $\beta$ is a holomorphic Poisson bivector field with respect to $\omega$, meaning that $[\beta, \beta]\omega = 0$ and $d^{0,2}\beta = 0$, where $[\cdot,\cdot]_\omega$ is the Schouten-Nijenhuis bracket and $d^{0,2}$ is the $(0,2)$ part of the de Rham differential.





The resulting types of $(\mathcal{J}_A, \mathcal{J}_B)$ depend on the type of $\beta$. If $\beta$ is of type $(1,1)$, then $\mathcal{J}_B$ is a complex structure and $\mathcal{J}_A$ is a deformation of this complex structure. If $\beta$ is of type $(2,0)$ or $(0,2)$, then $\mathcal{J}_B$ is a symplectic structure and $\mathcal{J}_A$ is a deformation of this symplectic structure. If $\beta$ is of mixed type, then $(\mathcal{J}_A, \mathcal{J}_B)$ form a bihermitian structure.






















问题 2. 





Let $\mathcal{J}$ be a generalized complex structure. Show that $e^{\theta \mathcal{J}}\left(T^*\right)$ is a Dirac structure for all $\theta$.





 
 




证明 . 





To show that $e^{\theta\mathcal{J}}(T^*)$ is a Dirac structure, we need to show that it is both isotropic and involutive.





Isotropy: Let $X, Y$ be two vector fields on $T^*$. We want to show that $e^{\theta\mathcal{J}}(X)\cdot e^{\theta\mathcal{J}}(Y)=0$, where $\cdot$ denotes the pairing between vectors and covectors.





Since $\mathcal{J}$ is a generalized complex structure, we know that it satisfies the following conditions:





    

  • $\mathcal{J}^2=-\mathrm{id}$
    • 




  • $\mathcal{J}$ preserves the natural symplectic structure on $T^$, i.e., $\mathcal{J}^ \omega = \omega$, where $\omega$ is the canonical symplectic form on $T^*$.
    • 






Using these conditions, we can compute the pairing between $e^{\theta\mathcal{J}}(X)$ and $e^{\theta\mathcal{J}}(Y)$ as follows:





\begin{align*} e^{\theta\mathcal{J}}(X) \cdot e^{\theta\mathcal{J}}(Y) &= \left\langle e^{\theta\mathcal{J}}(X),, \theta\mathcal{J}e^{\theta\mathcal{J}}(Y)\right\rangle\ &= \theta\left\langle \mathcal{J}e^{\theta\mathcal{J}}(X),, e^{\theta\mathcal{J}}(Y)\right\rangle\ &= \theta\left\langle e^{\theta\mathcal{J}}(\mathcal{J}X),, e^{\theta\mathcal{J}}(Y)\right\rangle\ &= \theta\left\langle \mathcal{J}X,, Y\right\rangle\ &= \theta\omega(X,, Y)\ &= 0, \end{align*}





where the third equality follows from the fact that $\mathcal{J}$ is a linear map and hence commutes with scalar multiplication, and the fourth equality follows from the fact that $e^{\theta\mathcal{J}}$ preserves the symplectic form $\omega$.





Thus, we have shown that $e^{\theta\mathcal{J}}(T^*)$ is isotropic.





Involutive: To show that $e^{\theta\mathcal{J}}(T^)$ is involutive, we need to show that for any two sections $x_1,x_2\in e^{\theta\mathcal{J}}(T^)$, their Lie bracket $[x_1,x_2]$ is also a section of $e^{\theta\mathcal{J}}(T^*)$.


















问题 3. 





What is the T-dual of the trivial $S^1$ bundle over $S^2$ with $H=k \nu$ where $k \in \mathbb{Z}$ and $\nu$ is the generator of $H^3\left(S^1 \times S^2, \mathbb{Z}\right)$ ?





 
 




证明 . 





To find the T-dual of the given bundle, we need to first compute the geometric data of the bundle, which includes the metric $g$ and the $B$-field. Then we apply the rules of T-duality to obtain the dual bundle.





The trivial $S^1$ bundle over $S^2$ can be described by the principal bundle $P=S^1\times S^2$ with the projection map $\pi:P\to S^2$. Let $e_1,e_2,e_3$ be the standard basis vectors of $\mathbb{R}^3$ and $x^i$ be the corresponding coordinates. We can choose the metric $g$ and the $B$-field $B$ on $P$ as follows:





$\begin{gathered}g=d x^2+\sin ^2(\theta) d \phi^2+\cos ^2(\theta) d \theta^2 \ B=k \cos (\theta) d \theta \wedge d \phi\end{gathered}$





where $\theta$ and $\phi$ are the usual spherical coordinates on $S^2$. Note that $g$ is a metric of constant curvature 1 and $B$ is a closed 2-form that represents the generator $\nu$ of $H^3(S^1\times S^2,\mathbb{Z})$.





To apply T-duality, we choose a circle direction to be dualized, say the $\phi$ direction. We replace the circle $S^1$ by its dual circle $\tilde{S}^1$, whose radius is given by the inverse of the original radius $R$. We also replace the $B$-field by its dual $\tilde{B}$, which is given by





$\tilde{B}=-\frac{k}{2 \pi R} \sin (\theta) d \theta \wedge d \phi$





where $\tilde{x}^i$ are the coordinates of $\tilde{P}$, and $e_\phi^i$ is the $\phi$ component of the basis vectors of $\mathbb{R}^3$. The new metric $\tilde{g}$ on $\tilde{P}$ is given by





$\tilde{g}=\frac{R}{\sin (\theta)}\left(d \tilde{x}^2+\cos ^2(\theta) d \tilde{\theta}^2+\sin ^2(\theta) d \tilde{\phi}^2\right)$





where $\tilde{\theta}$ and $\tilde{\phi}$ are the coordinates of $\tilde{S}^2$. Note that $\tilde{g}$ is again a metric of constant curvature 1. Therefore, the T-dual of the trivial $S^1$ bundle over $S^2$ with $H=k\nu$ is the trivial $\tilde{S}^1$ bundle over




















这是一份2023年的波士顿学院Boston College MATH 8831几何学/拓扑学代写的成功案例