这是一份andrews圣安德鲁斯大学 MT3505作业代写的成功案例
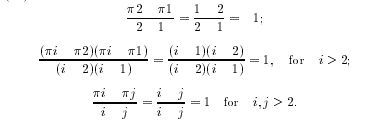
Proof. Multiplication in $R / A$ is well-defined, since if $r_{1}+A=r_{1}^{\prime}+A$ and $r_{2}+A=r_{2}^{\prime}+A$, then writing $r_{i}^{\prime}=r_{i}+a_{i}$ for $a_{i}$ in $A$ we see
$$
\begin{aligned}
r_{1}^{\prime} r_{2}^{\prime}+A &=\left(r_{1}+a_{1}\right)\left(r_{2}+a_{2}\right)+A \
&=r_{1} r_{2}+\left(r_{1} a_{2}+a_{1} r_{2}+a_{1} a_{2}\right)+A=r_{1} r_{2}+A .
\end{aligned}
$$
Associativity and distributivity are easy to verify in $R / A$, as a consequence of the respective axioms in $R$. Moreover,
$$
(1+A)(r+A)=r+A=(r+A)(1+A),
$$
so $1+A$ is the unit element of $R / A$. We already know $\varphi$ is a group homomorphism with respect to $+$, and $\varphi(1)=1+A$, and
$$
\varphi\left(r_{1}\right) \varphi\left(r_{2}\right)=\left(r_{1}+A\right)\left(r_{2}+A\right)=r_{1} r_{2}+A=\varphi\left(r_{1} r_{2}\right)
$$

MT3505 COURSE NOTES :
For per haps a thousand years or more, one of the major research questions in mathematics was to solve the general cubic equation
$$
x^{3}+b x^{2}+c x+d=0 .
$$
In analogy to the quadratic case, one can obtain the simpler equation
$$
y^{3}+p y+q=0,
$$