这是一份umass麻省大学 MATH 671作业代写的成功案例
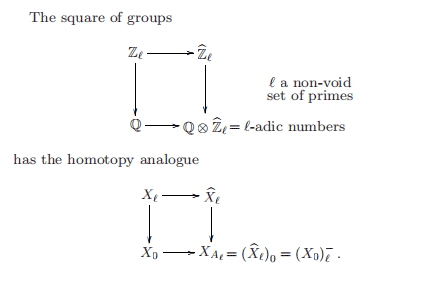
So map each simplex in the first barycentric subdivision of $K$,
$$
\sigma_{1}<\sigma_{2}<\cdots<\sigma_{n}, \quad \sigma_{i} \in K
$$
to the simplex in nerve $C(U)$,
$$
U_{\sigma_{n}} \subseteq U_{\sigma_{n-1}} \subseteq \cdots \subseteq U_{\sigma_{1}}
$$
This gives a simplicial map
$K^{\prime} \rightarrow \vec{g}$ nerve $C(U), K^{\prime}=1$ st barycentric subdivision $.$
Now consider the compositions
$$
\begin{aligned}
&K^{\prime} \underset{g}{\rightarrow} \text { nerve } C(U) \underset{f}{\rightarrow} K \
&\text { nerve } C(U) \stackrel{f}{\rightarrow} K=K^{\prime} \stackrel{g}{\rightarrow} \text { nerve } C(U)
\end{aligned}
$$
One can check for the first composition that a simplex of $K^{\prime}$
$$
\sigma_{1}<\cdots<\sigma_{n}
$$

MATH 671 COURSE NOTES :
(the two sphere, $S^{2}$ ) Let $p$ and $\sigma$ denote two distinct points of $S^{2}$. Consider the category over $S^{2}$ determined by the maps
$$
\begin{array}{cc}
\text { object } & \text { name } \
S^{2}-p \stackrel{\subseteq}{\longrightarrow} S^{2} & e \
S^{2}-q \subseteq S^{2} & e^{\prime} \
\text { (universal cover } \left.S^{2}-p-q\right) \rightarrow S^{2} & \mathbb{Z} .
\end{array}
$$
The category has three objects and might be denoted