这是一份umass麻省大学 MATH 551作业代写的成功案例
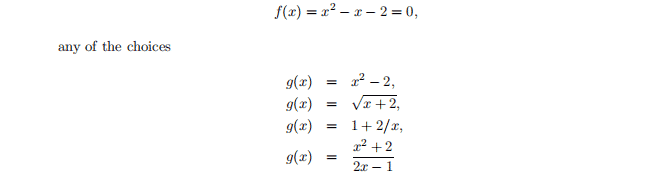

The proof of this result is simple and instructive, so we sketch it here. If $x^{}$ is a fixed point, then for the error at the $k$ th iteration we have $$ e_{k+1}=x_{k+1}-x^{}=g\left(x_{k}\right)-g\left(x^{}\right) $$ By the Mean Value Theorem, there is a point $\theta_{k}$ between $x_{k}$ and $x^{}$ such that
$$
g\left(x_{k}\right)-g\left(x^{}\right)=g^{\prime}\left(\theta_{k}\right)\left(x_{k}-x^{}\right)
$$
so that
$$
e_{k+1}=g^{\prime}\left(\theta_{k}\right) e_{k}
$$
We do not know the value of $\theta_{k}$, but if $\left|g^{\prime}\left(x^{}\right)\right|<1$, then by starting the iterations close enough to $x^{}$, we can be assured that there is a constant $C$ such that $\left|g^{\prime}\left(\theta_{k}\right)\right| \leq C<1$, for $k=0,1, \ldots$ Thus, we have
$$
\left|e_{k+1}\right| \leq C\left|e_{k}\right| \leq \cdots \leq C^{k}\left|e_{0}\right|
$$
and since $C^{k} \rightarrow 0$, then $\left|e_{k}\right| \rightarrow 0$ and the sequence converges.

MATH 551 COURSE NOTES :
Newton’s Method. We illustrate Newton’s method by again finding a root of the equation
$$
f(x)=x^{2}-4 \sin (x)=0 .
$$
The derivative of this function is given by
$$
f^{\prime}(x)=2 x-4 \cos (x),
$$
so that the iteration scheme is given by
$$
x_{k+1}=x_{k}-\frac{x_{k}^{2}-4 \sin \left(x_{k}\right)}{2 x_{k}-4 \cos \left(x_{k}\right)} .
$$