这是一份试验设计与方差分析作业代写的成功案
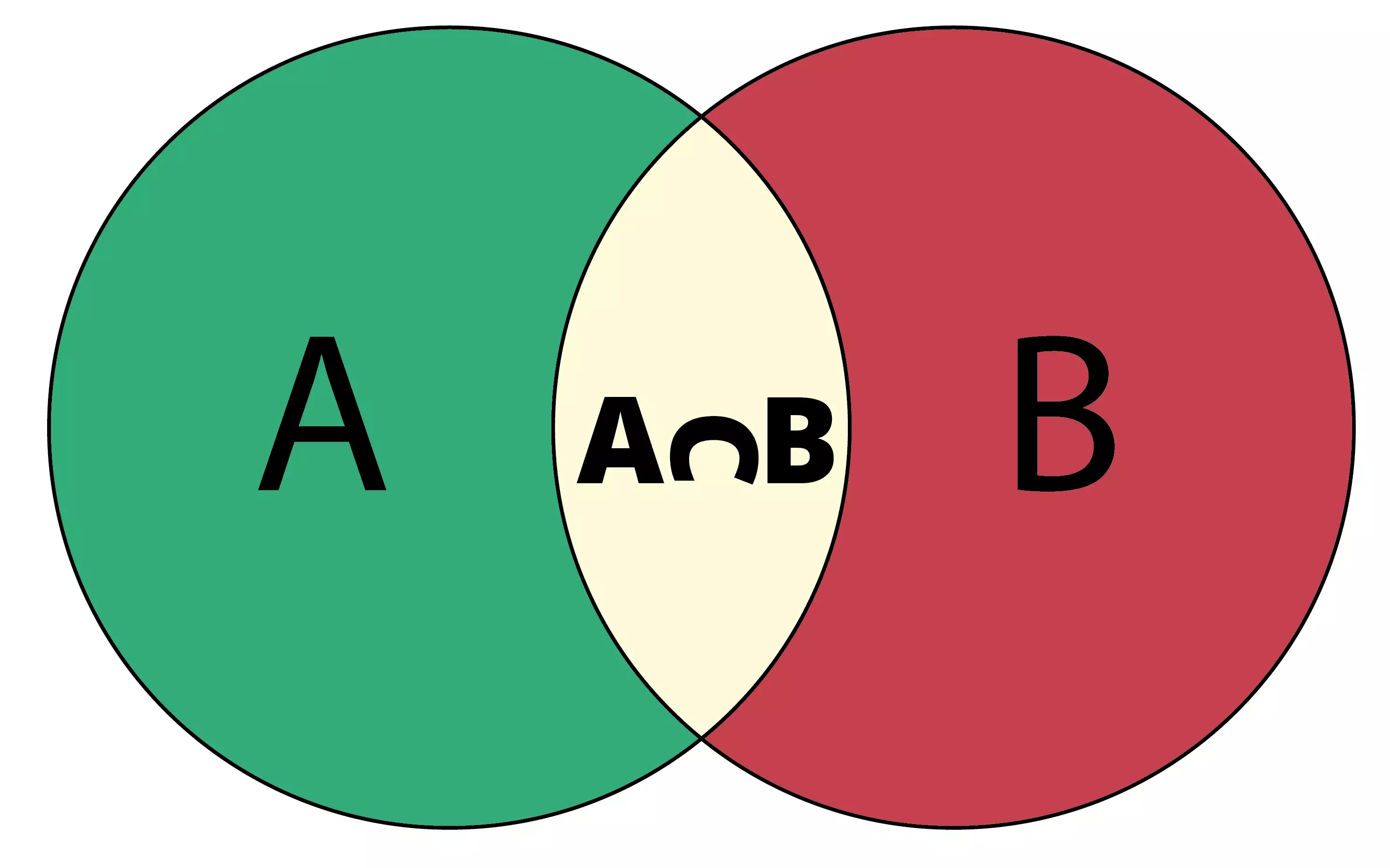
$$
P\left[\lim {n \rightarrow \infty} X{n}=0\right]=1
$$
if
$$
\sum_{n} p_{n}<\infty
$$
To verify that observe that if
$$
\sum_{n} p_{n}=\sum_{n} P\left[X_{n}=1\right]<\infty,
$$
then by the Borel-Cantelli Lemma
$$
P\left(\left[X_{n}=1\right] \text { i.o. }\right)=0
$$
Taking complements, we find
$$
1=P\left(\limsup {n \rightarrow \infty}\left[X{n}=1\right]^{c}\right)=P\left(\liminf {n \rightarrow \infty}\left[X{n}=0\right]\right)=1 .
$$

Math 425/Math 340 / Stat 231/ST 8553/Math 551/MA 485/585COURSE NOTES :
$$
P\left[X_{k}=1\right]=p_{k}=1-P\left[X_{k}=0\right]
$$
Then we assert that
$$
P\left[X_{n} \rightarrow 0\right]=1 \text { iff } \sum_{n} p_{k}<\infty
$$
To verify this assertion, we merely need to observe that
$$
P\left{\left[X_{n}=1\right] \text { i.o. }\right}=0
$$
iff
$$
\sum_{n} P\left[X_{n}=1\right]=\sum_{n} p_{n}<\infty
$$