Assignment-daixieTM为您提供布里斯托大学University of Bristol Foundation Classical Physics II: Electromagnetism and Waves PHYS20020电磁学和电波代写代考和辅导服务!
Instructions:
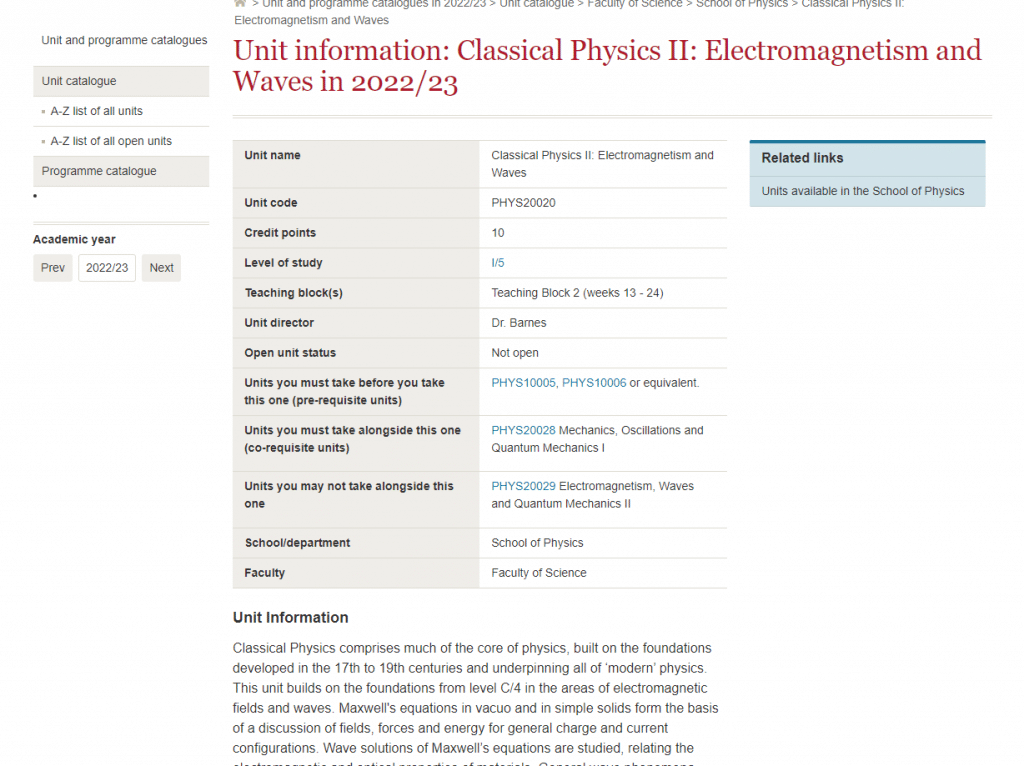
Classical Physics is a branch of physics that deals with the study of macroscopic phenomena at speeds much slower than the speed of light. It was developed in the 17th to 19th centuries and forms the foundation of modern physics. The core concepts of classical physics include mechanics, thermodynamics, electromagnetism, and optics.
This unit builds on the foundations developed in level C/4 in the areas of electromagnetic fields and waves. Maxwell’s equations, which describe the behavior of electric and magnetic fields, are studied in vacuo and in simple solids. These equations form the basis of a discussion of fields, forces, and energy for general charge and current configurations.
The wave solutions of Maxwell’s equations are also studied in this unit. These solutions relate the electromagnetic and optical properties of materials, providing a deeper understanding of how light interacts with matter. General wave phenomena, such as interference and diffraction, are investigated, along with practical applications of these effects.
Overall, this unit provides a comprehensive understanding of electromagnetic fields and waves, which is essential for understanding many aspects of modern physics and technology.
Use index notation to derive a formula for $\vec{\nabla} \times(s \vec{A})$, where $s$ is a scalar field $s(\vec{r})$ and $\vec{A}$ is a vector field $\vec{A}(\vec{r})$.
$\begin{aligned} {[\vec{\nabla} \times(s \vec{A})]i } & =\varepsilon{i j k} \partial_j(s \vec{A})k \ & =\varepsilon{i j k} s \partial_j A_k+\varepsilon_{i j k} A_k \partial_j s \ & =s \vec{\nabla} \times \vec{A}+\vec{\nabla} s \times \vec{A} .\end{aligned}$
Which of the following vector fields could describe an electric field? Say yes or no for each, and give a very brief reason.
(i) $\vec{E}(\vec{r})=x \hat{e}_x-y \hat{e}_y$.
(ii) $\vec{E}(\vec{r})=y \hat{e}_x+x \hat{e}_y$.
(iii) $\vec{E}(\vec{r})=y \hat{e}_x-x \hat{e}_y$.
The curl of an electrostatic field must be zero, but otherwise there is no restriction. So the answer follows as
(i) $\vec{\nabla} \times \vec{E}(\vec{r})=\left(\frac{\partial E_y}{\partial x}-\frac{\partial E_x}{\partial y}\right) \hat{e}_z+\ldots=\overrightarrow{0}$. YES, it describes an electric field.
(ii) $\vec{\nabla} \times \vec{E}(\vec{r})=(1-1) \hat{e}_z=0$. YES, it describes an electric field.
(iii) $\vec{\nabla} \times \vec{E}(\vec{r})=(-1-1) \hat{e}_z=-2 \hat{e}_z$. NO, it does not describe an electric field.
(a) A spherical shell of radius $R$, with an unspecified surface charge density, is centered at the origin of our coordinate system. The electric potential on the shell is known to be
$$
V(\theta, \phi)=V_0 \sin \theta \cos \phi,
$$
where $V_0$ is a constant, and we use the usual polar coordinates, related to the Cartesian coordinates by
$$
\begin{aligned}
& x=r \sin \theta \cos \phi, \
& y=r \sin \theta \sin \phi, \
& z=r \cos \theta .
\end{aligned}
$$
Find $V(r, \theta, \phi)$ everywhere, both inside and outside the sphere. Assume that the zero of $V$ is fixed by requiring $V$ to approach zero at spatial infinity. (Hint: this problem can be solved using traceless symmetric tensors, or if you prefer you can use standard spherical harmonics. A table of the low- $\ell$ Legendre polynomials and spherical harmonics is included with the formula sheets.)
This problem can be solving using either traceless symmetric tensors or the more standard spherical harmonics. I will show the solution both ways, starting with the simplier derivation in terms of traceless symmetric tensors.
(a) We exploit the fact that the most general solution to Laplace’s equation can be written as a sum of terms of the form
$$
\left(r^{\ell} \text { or } \frac{1}{r^{\ell+1}}\right) C_{i_1 \ldots i_{\ell}}^{(\ell)} \hat{n}{i_1} \ldots \hat{n}{i_{\ell}},
$$
where $C_{i_1 \ldots i_{\ell}}^{(\ell)}$ is a traceless symmetric tensor. In this case we only need an $\ell=1$ term, since
$$
F_a(\theta, \phi) \equiv \sin \theta \cos \phi=\frac{x}{r}=\hat{x}_i \hat{n}_i
$$
For $\ell=1$ the radial function must be $r$ or $1 / r^2$. For $rR$ the term proportional to $r$ is excluded, because it does not approach zero as $r \rightarrow \infty$, so only the $1 / r^2$ option remains, and the solution is
$$
\begin{aligned}
V(\vec{r}) & =V_0\left(\frac{R}{r}\right)^2 F_a(\theta, \phi) \
& =V_0\left(\frac{R}{r}\right)^2 \hat{x}_i \hat{n}_i \text { or } V_0\left(\frac{R}{r}\right)^2 \sin \theta \cos \phi .
\end{aligned}
$$
