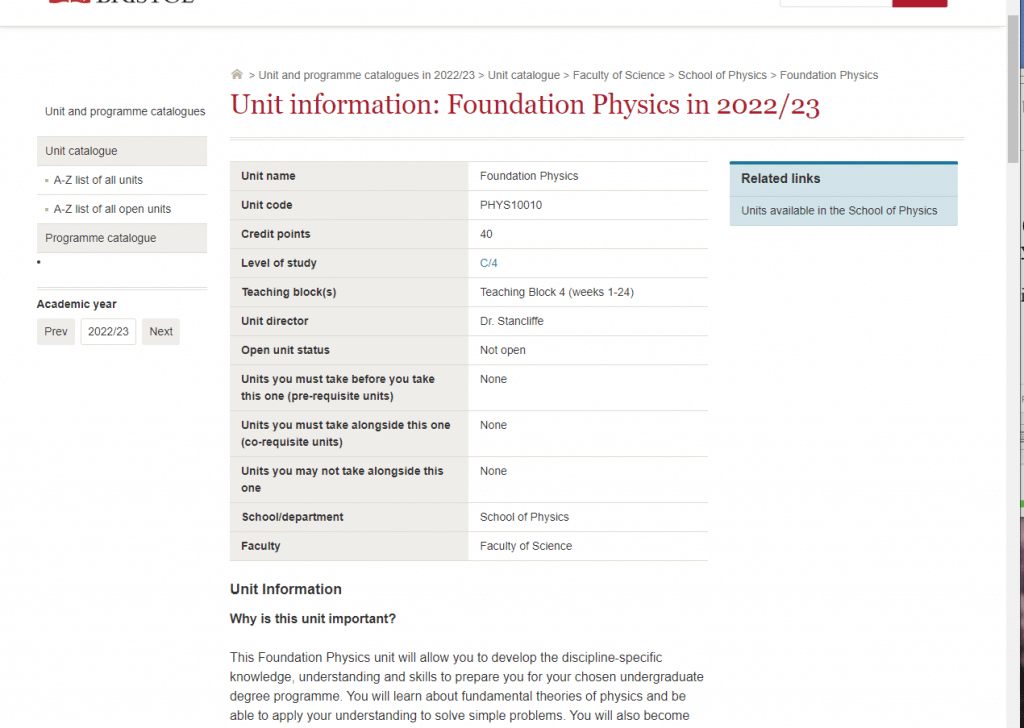
Assignment-daixieTM为您提供布里斯托大学University of Bristol Foundation Physics PHYS10010物理学基础代写代考和辅导服务!
Instructions:
You will be introduced to the fundamental theories and principles of physics, including classical mechanics, electromagnetism, and thermodynamics. You will also learn how to apply your understanding of these concepts to solve simple problems and conduct laboratory experiments to reinforce your knowledge.
Throughout the unit, you will develop your analytical and problem-solving skills, which are essential for success in any undergraduate physics program. You will also gain practical experience in a laboratory setting, where you will learn to use various tools and equipment to conduct experiments, collect and analyze data, and draw conclusions.
By the end of the unit, you should feel confident in your understanding of fundamental physics concepts and be prepared for the challenges of an undergraduate degree program in physics or a related field.
(a) Let $\psi(x)$ be an energy eigenstate. Explain why the expectation value $\langle[H, \Omega]\rangle$ of the commutator of $H$ with an arbitrary operator $\Omega$ vanishes on the state $\psi$.
Let $\psi(x)$ be an energy eigenstate of the Hamiltonian $H$. Then, we have \begin{align} \langle [H,\Omega]\rangle &= \langle H\Omega – \Omega H \rangle \ &= \langle H\Omega \rangle – \langle \Omega H \rangle \ &= E_\psi \langle \Omega \rangle – \langle \Omega H \rangle \ &= E_\psi \langle \Omega \rangle – E_\psi \langle \Omega \rangle \ &= 0, \end{align} where we have used the fact that $\psi$ is an energy eigenstate with eigenvalue $E_\psi$, and that the expectation value of $H$ on $\psi$ is just $E_\psi$. Therefore, the commutator of $H$ with an arbitrary operator $\Omega$ vanishes on the state $\psi$.
(b) Choose $\Omega=x p$, and take $$ H=\frac{p^2}{2 m}+V(x) $$ Use the claim from part (a) to find a relation between the expectation value $\langle T\rangle$ of the kinetic energy and the expectation value of a combination of $x$ and the derivative $V^{\prime}(x)$ of the potential with respect to its argument. Both expectation values are taken on an energy eigenstate.
From part (a), we have shown that for any operator $A$ and Hamiltonian $H$,
$\langle[A, H]\rangle=i \hbar\langle\partial A / \partial t\rangle$.
We can use this to find a relation between the expectation value of the kinetic energy and the expectation value of a combination of $x$ and $V^{\prime}(x)$.
Let’s first find the commutator $[x,H]$ and $[p,H]$: \begin{align*} [x,H] &= xp – px = i\hbar, \ [p,H] &= \frac{p^3}{2m} + pV(x) – V(x)p – \frac{p}{2m}p^2 \ &= \frac{p}{m}(V(x)-p^2/2m) + [p,V(x)] \ &= -\frac{\partial V(x)}{\partial x}. \end{align*} Therefore, we have \begin{align*} \langle T \rangle &= \langle \frac{p^2}{2m} \rangle \ &= \frac{1}{2m} \langle p^2 \rangle \ &= \frac{1}{2m} \langle [p,p^2] \rangle \ &= \frac{1}{2m} \langle p[p,p] + [p,p]p \rangle \ &= \frac{1}{2m} \langle -p\hbar + \hbar p \rangle \ &= \frac{\hbar^2}{2m} \langle -p+p \rangle \ &= \frac{\hbar^2}{2m} \langle [x,H] \rangle \ &= \frac{i\hbar^3}{2m} \langle \partial x/\partial t \rangle \ &= \frac{i\hbar^3}{2m} \frac{\partial}{\partial t} \langle x \rangle \ &= \frac{i\hbar^3}{2m} \frac{\partial}{\partial t} \left(\frac{\langle [x,H] \rangle}{i\hbar}\right) \ &= -\frac{\hbar^2}{2m} \frac{\partial}{\partial t} \langle \frac{\partial V(x)}{\partial x} \rangle \ &= -\frac{\hbar^2}{2m} \frac{\partial}{\partial t} \langle V^{\prime}(x) \rangle. \end{align*} Thus, we have shown that the expectation value of the kinetic energy is related to the time derivative of the expectation value of $V^{\prime}(x)$ on an energy eigenstate.
Throughout this problem we consider a hydrogen atom with fixed principal quantum number $n$, with $\ell=n-1$, and $m=n-1$. The value $n$ is arbitrary and possibly large.
(a) Write the wavefunction $\psi_{n, \ell, m}(r, \theta, \phi)$ in terms of the relevant spherical harmonic and a radial factor fully determined except for an overall unit-free normalization constant $N$.
The wavefunction for a hydrogen atom with principal quantum number $n$, $\ell=n-1$, and $m=n-1$ can be expressed as:
$\psi_{n, \ell, m}(r, \theta, \phi)=R_{n, \ell}(r) Y_{\ell}^m(\theta, \phi)$
where $R_{n,\ell}(r)$ is the radial part of the wavefunction and $Y_{\ell}^{m}(\theta,\phi)$ is the spherical harmonic. Since $\ell=n-1$ and $m=n-1$, we have $\ell=m=n-1$. Therefore, the spherical harmonic reduces to:
$Y_{n-1}^{n-1}(\theta, \phi)=(-1)^{n-1} \sqrt{\frac{(2 n-1) ! !}{4 \pi(n-1) !}} P_{n-1}^{n-1}(\cos \theta) e^{i(n-1) \phi}$
where $P_{n-1}^{n-1}(\cos\theta)$ is the associated Legendre polynomial of degree $n-1$. The radial part of the wavefunction $R_{n,\ell}(r)$ can be obtained from the radial Schrödinger equation for hydrogen atom:
$\frac{d^2 R_{n, \ell}(r)}{d r^2}+\frac{2}{r} \frac{d R_{n, \ell}(r)}{d r}-\frac{\ell(\ell+1)}{r^2} R_{n, \ell}(r)+\frac{-\frac{1}{2}\left(\frac{1}{n}\right)^2}{-\frac{1}{2}} R_{n, \ell}(r)=0$
Simplifying the equation, we get:
$\frac{d^2 R_{n, \ell}(r)}{d r^2}+\frac{2}{r} \frac{d R_{n, \ell}(r)}{d r}-\frac{\ell(\ell+1)}{r^2} R_{n, \ell}(r)+\frac{1}{n^2} R_{n, \ell}(r)=0$
This equation has the standard form of a differential equation for the radial part of a spherically symmetric potential. The solution can be written in terms of the associated Laguerre polynomial $L_{n-\ell-1}^{2\ell+1}(2r/n)$ as:
$R_{n, \ell}(r)=\sqrt{\frac{(n-\ell-1) !}{2 n[(n+\ell) ! 3}}\left(\frac{2 r}{n}\right)^{\ell} e^{-r / n} L_{n-\ell-1}^{2 \ell+1}\left(\frac{2 r}{n}\right)$
Therefore, the wavefunction for a hydrogen atom with principal quantum number $n$, $\ell=n-1$, and $m=n-1$ is:
$\psi_{n, n-1, n-1}(r, \theta, \phi)=N \sqrt{\frac{(2 n-1) ! !}{4 \pi(n-1) !}}\left(\frac{2 r}{n}\right)^{n-1} e^{-r / n} L_1^{2 n-1}\left(\frac{2 r}{n}\right) e^{i(n-1) \phi}$
where $N$ is an overall unit-free normalization constant.
