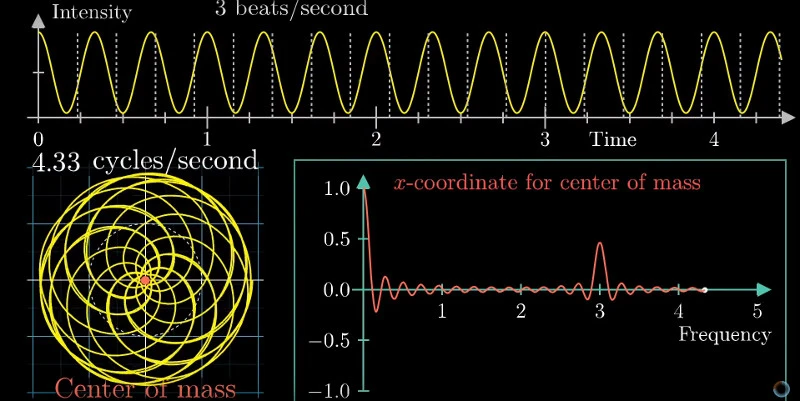
Understand the statements and proofs of important theorems and be able to explain the key steps in proofs, sometimes with variation.
这是一份drps.ed爱丁堡个大学MATH10051作业代写的成功案
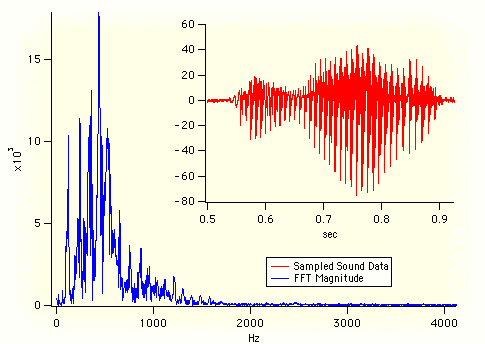
To do this we introduce complex numbers by adding $i$ times the second equation to the first to obtain the single equation
$$
\frac{d}{d t}(U+i V)=B(V-i U) .
$$
If we set $\Phi=U+i V$ this equation takes the form
$$
\dot{\Phi}=-i B \Phi
$$
This is an equation that we can solve to obtain
$$
\Phi(t)=A e^{-i B t}
$$
where $A$ is a fixed complex number.
How does this solution fit in with our original problem. recall that we can write
$$
A=r \exp i \alpha
$$

MATH10051 COURSE NOTES :
If $x=R \cos \theta, y=R \sin \theta$ where $R$ is very large then to a very good approximation
$$
S(R \cos \theta, R \sin \theta, t)=R^{-2} \exp (i(\omega t-\lambda R) Q(u)
$$
where
$$
Q(u)=\sum_{k=-N}^{N} A_{k} \exp \left(i\left(k u-\phi_{k}\right)\right)
$$
and $u=\lambda^{-1} l \sin \theta$.
In the discussion that follows we use the notation of Lemma $4.1$ and the discussion that preceded it. We set
$$
P(u)=\sum_{k=-N}^{N} A_{k} \exp (i k u)
$$