这是一份bath巴斯大学PH30101作业代写的成功案

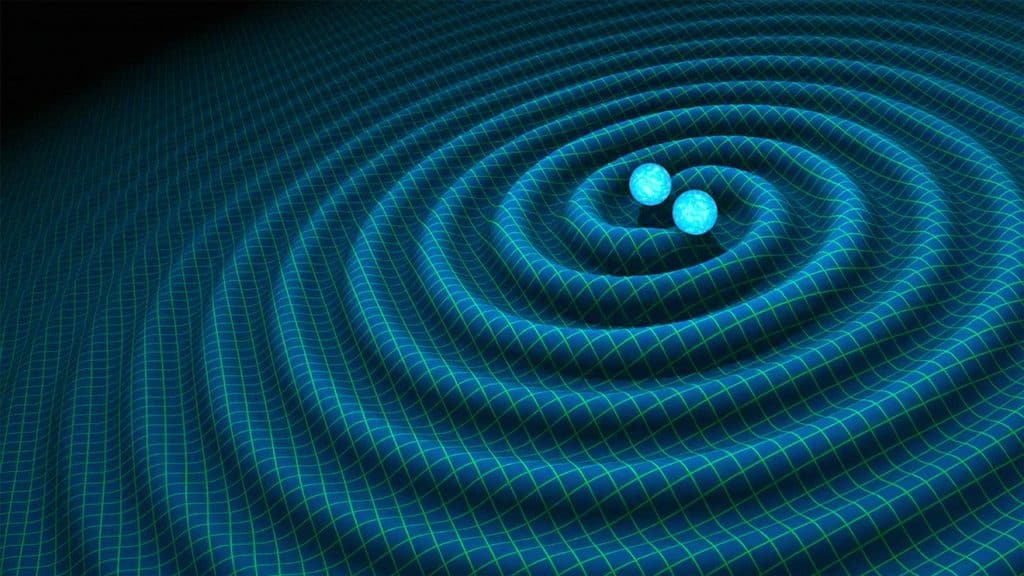
the corresponding null geodesics are
$$
\begin{aligned}
&\gamma_{X}: x^{A A^{\prime}} \equiv x_{0}^{A A^{\prime}}+\lambda \bar{X}^{A} X^{A^{\prime}} \
&\gamma_{Y}: x^{A A^{\prime}} \equiv x_{1}^{A A^{\prime}}+\mu \bar{Y}^{A} Y^{A^{\prime}}
\end{aligned}
$$
If these intersect at some point, say $x_{2}$, one finds
$$
x_{2}^{A A^{\prime}}=x_{0}^{A A^{\prime}}+\lambda \bar{X}^{\mathcal{A}} X^{A^{\prime}}=x_{1}^{A A^{\prime}}+\mu \bar{Y}^{A} Y^{A^{\prime}}
$$
where $\lambda \mu \in R$. Hence
$$
x_{2}^{A A^{\prime}} \bar{Y}{A} X{A^{\prime}}=x_{0}^{A A^{\prime}} \bar{Y}{A} X{A^{\prime}}=x_{1}^{A A^{\prime}} \bar{Y}{A} X{A^{\prime}}
$$

PH30101 COURSE NOTES ：

This enables one to define the spinor field
$$
p^{A} \equiv p^{A A^{\prime} B^{\prime}} \pi_{A^{\prime}} \pi_{B^{\prime}}
$$
and the patching function
$$
f^{A} \equiv p^{A} g\left(p_{B} \omega^{B}, \pi_{B^{\prime}}\right)
$$
and the function
$$
F\left(x^{a}, \pi_{A^{\prime}}\right) \equiv g\left(i p_{A} x^{A C^{\prime}} \pi_{C^{\prime}}, \pi_{A^{\prime}}\right)
$$