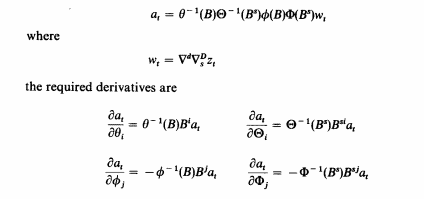
$$
\beta_{t}=\phi_{x}(B) \theta_{x}^{-1}(B) y_{t}
$$
then the model may be written
$$
\beta_{t}=v(B) \alpha_{t}+\varepsilon_{t}
$$
where $\varepsilon_{t}$ is the transformed noise series defined by
$$
\varepsilon_{t}=\phi_{x}(B) \theta_{x}^{-1}(B) n_{t}
$$
$$
\gamma_{\alpha \beta}(k)=v_{k} \sigma_{\alpha}^{2}
$$
where $\gamma_{\alpha \beta}(k)=E\left[\alpha_{t-k} \beta_{t}\right]$ is the cross covariance at lag $+k$ between $\alpha$ and $\beta$. Thus
$$
v_{k}=\frac{\gamma_{\alpha \phi}(k)}{\sigma_{\alpha}^{2}}
$$

6CCM344A COURSE NOTES :
$$
f_{1, t}=\delta_{1}^{-1}(B) \omega_{1}(B) x_{1, t-b_{1}}
$$
and for specified values of $b_{2}, \boldsymbol{\delta}{2}, \boldsymbol{\omega}{2}$,
$$
y_{2, t}=\delta_{2}^{-1}(B) \omega_{2}(B) x_{2, t-b_{2}}
$$
Then the noise $n_{t}$ can be calculated from
$$
n_{t}=y_{t}-y_{1, t}-y_{2, t}
$$
and finally, $a_{t}$ from
$$
a_{t}=\theta^{-1}(B) \phi(B) n_{t}
$$