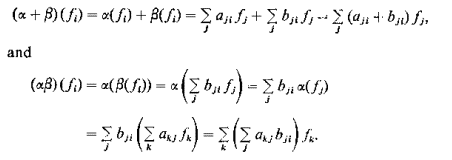
Proof. (i) It is most convenient here to think in module terms. We have $V=V_{1} \oplus \cdots \oplus V_{s}$ as $\mathbf{k}[x]$-module, where $V_{1}$ is cyclic of order $d_{i}$. As $d_{i} \mid d_{s}$, we have $d_{s} V_{i}={0}$ for $1 \leqslant i \leqslant s$, and so $d_{s} V={0}$. Therefore $d_{s}(\alpha)=0$ and $g \mid d_{s}$, where $g=\min \alpha$. On the other hand, $g(\alpha)=0$, and so ${0}=g(\alpha) V_{s}=g V_{s^{*}}$. Hence $d_{s} \mid g$. Therefore $d_{s} \sim g$, and since $d_{s}$ and $g$ are both monic, this gives $d_{s}=g$.
We prove by induction on $r$ that $\operatorname{ch} C(d)=d$. If $r=1$, then the above determinant is equal to $x+a_{0}$ as stated. If $r>1$, we expand by the top row and obtain
$$
\begin{aligned}
\operatorname{ch} C\left(a_{0}+a_{1} x+\cdots+a_{r-1} x^{r-1}+x^{r}\right) \
&=x \operatorname{ch} C\left(a_{1}+a_{2} x+\cdots+a_{r-1} x^{r-2}+x^{r-1}\right)+a_{0}
\end{aligned}
$$
whence the result follows by induction.
We therefore obtain $\operatorname{ch} \alpha=\operatorname{ch} A=\operatorname{ch} C\left(d_{1}\right) \ldots \operatorname{ch} C\left(d_{s}\right)=d_{1} \ldots d_{s}$, as stated.

6CCM350A COURSE NOTES :
Proof. We notice first that a gencral element $f \in F$ has the form $f=\sum_{i=1}^{t} g_{i}(x) f_{i}$ with $g_{i}(x) \in \mathbf{k}[x]$, and that the effect of $\epsilon$ on such an element is given by
$$
\epsilon\left(\sum g_{i}(x) f_{i}\right)=\sum g_{i}(x) v_{l}=\sum g_{i}(\alpha)\left(v_{l}\right) .
$$
Therefore $\epsilon\left(n_{j}\right)=\alpha\left(v_{l}\right)-\sum a_{j i} v_{j}=0$, since $A=M(\alpha, v)$. Hence each $n_{i}$ belongs to $N$.
We now show that n generates $N$. To see this, let $N^{}$ be the submodule $\sum_{i=1}^{t} \mathbf{k}[x] n_{i}$ generated by $\mathbf{n}$. Then $$ N^{} \subseteq N \text {. }
$$