Assignment-daixieTM为您提供格拉斯哥大学University of Glasgow LINEAR ALGEBRA MATHS2004线性代数代写代考和辅导服务!
Instructions:
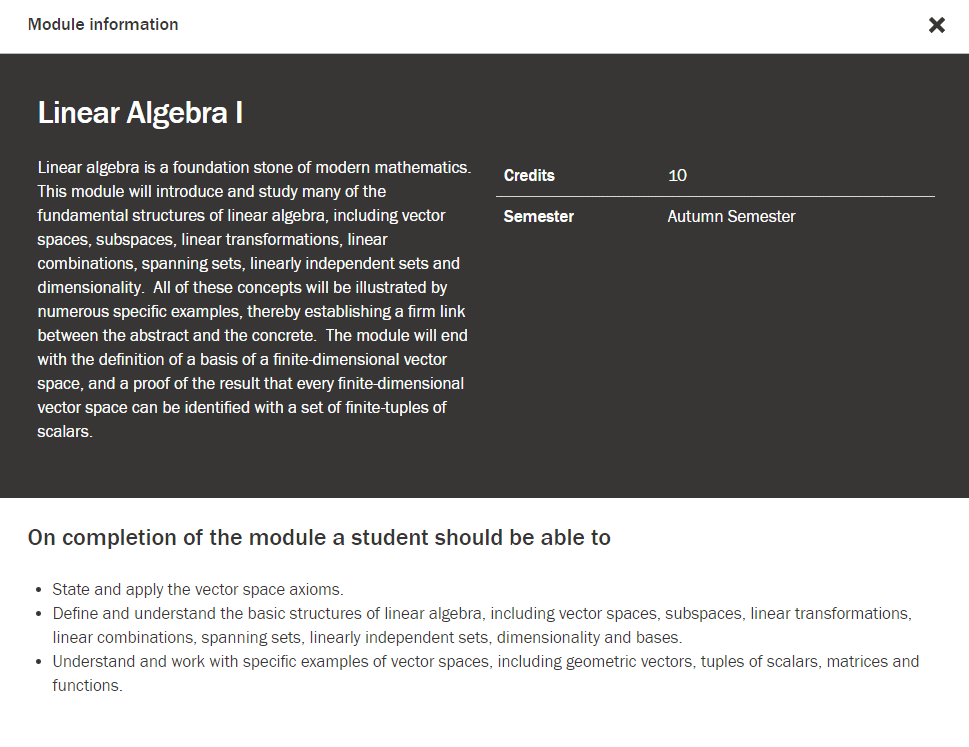
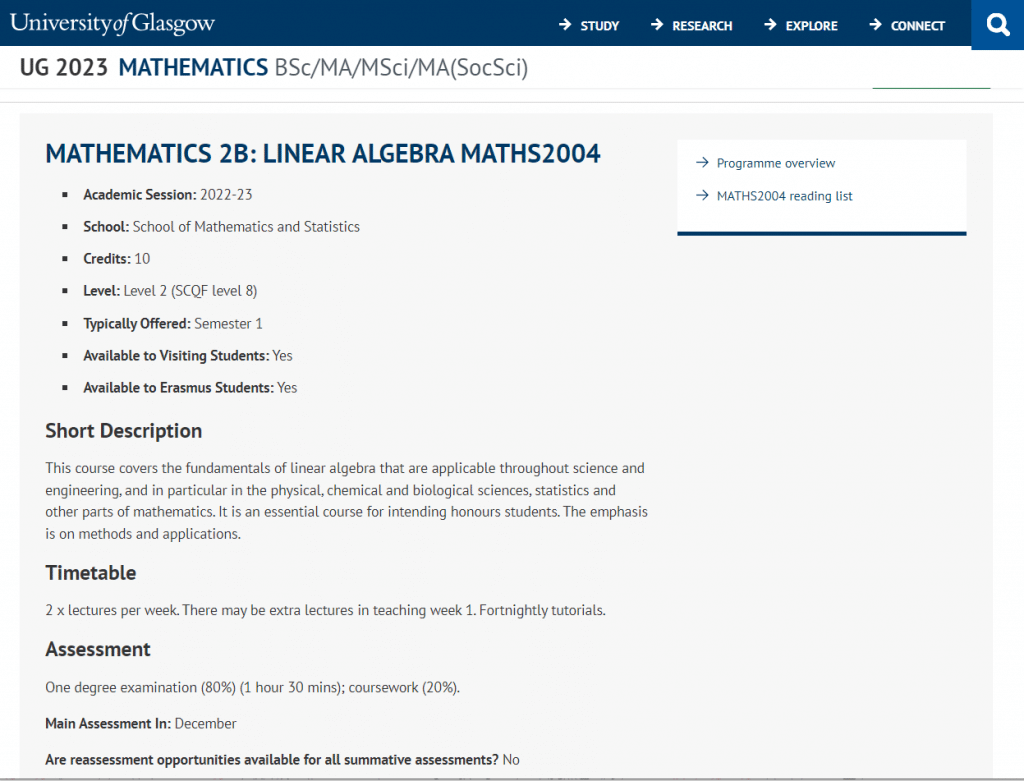
Linear algebra is a branch of mathematics that deals with vector spaces and linear equations, and it has many practical applications in fields such as physics, computer science, economics, and more.
Throughout this course, you can expect to learn about the basics of linear algebra, such as vectors, matrices, and systems of linear equations. You will also learn about more advanced topics, such as eigenvalues and eigenvectors, linear transformations, and inner products. By the end of the course, you should be able to apply these concepts to solve a variety of problems in different areas of science and engineering.
It’s great that this course is emphasizing methods and applications, as it will help you develop the skills you need to use linear algebra in real-world situations. This course will be particularly important for students who plan to pursue honors-level studies in these fields, as it will provide them with a strong foundation in linear algebra that they can build upon in future courses.
(b) Find the coefficients $C$ and $D$ of the best curve $y=C+D 2^t$.
$$
\begin{gathered}
A^T A=\left[\begin{array}{lll}
1 & 1 & 1 \
1 & 2 & 4
\end{array}\right]\left[\begin{array}{ll}
1 & 1 \
1 & 2 \
1 & 4
\end{array}\right]=\left[\begin{array}{lc}
3 & 7 \
7 & 21
\end{array}\right] \
A^T b=\left[\begin{array}{lll}
1 & 1 & 1 \
1 & 2 & 4
\end{array}\right]\left[\begin{array}{l}
6 \
4 \
0
\end{array}\right]=\left[\begin{array}{l}
10 \
14
\end{array}\right]
\end{gathered}
$$
Solve $A^T A \hat{x}=A^T b$ :
$$
\left[\begin{array}{cc}
3 & 7 \
7 & 21
\end{array}\right]\left[\begin{array}{l}
C \
D
\end{array}\right]=\left[\begin{array}{l}
10 \
14
\end{array}\right] \text { gives }\left[\begin{array}{l}
C \
D
\end{array}\right]=\frac{1}{14}\left[\begin{array}{rr}
21 & -7 \
-7 & 3
\end{array}\right]\left[\begin{array}{l}
10 \
14
\end{array}\right]=\left[\begin{array}{r}
8 \
-2
\end{array}\right]
$$
(a) Suppose $x_k$ is the fraction of MIT students who prefer calculus to linear algebra at year $k$. The remaining fraction $y_k=1-x_k$ prefers linear algebra.
At year $k+1,1 / 5$ of those who prefer calculus change their mind (possibly after taking 18.03). Also at year $k+1,1 / 10$ of those who prefer linear algebra change their mind (possibly because of this exam).
Create the matrix $A$ to give $\left[\begin{array}{l}x_{k+1} \ y_{k+1}\end{array}\right]=A\left[\begin{array}{l}x_k \ y_k\end{array}\right]$ and find the limit of $A^k\left[\begin{array}{l}1 \ 0\end{array}\right]$ as $k \rightarrow \infty$.
$$
A=\left[\begin{array}{ll}
.8 & .1 \
.2 & .9
\end{array}\right] .
$$
The eigenvector with $\lambda=1$ is $\left[\begin{array}{l}1 / 3 \ 2 / 3\end{array}\right]$.
This is the steady state starting from $\left[\begin{array}{l}1 \ 0\end{array}\right]$.
$\frac{2}{3}$ of all students prefer linear algebra! I agree.
Solve these differential equations, starting from $x(0)=1, \quad y(0)=0$ :
$$
\frac{d x}{d t}=3 x-4 y \quad \frac{d y}{d t}=2 x-3 y
$$
$$
A=\left[\begin{array}{ll}
3 & -4 \
2 & -3
\end{array}\right]
$$
has eigenvalues $\lambda_1=1$ and $\lambda_2=-1$ with eigenvectors $x_1=(2,1)$ and $x_2=(1,1)$. The initial vector $(x(0), y(0))=(1,0)$ is $x_1-x_2$.
So the solution is $(x(t), y(t))=e^t(2,1)+e^{-t}(1,1)$.