这是一份umass麻省大学 MATH 597U作业代写的成功案例
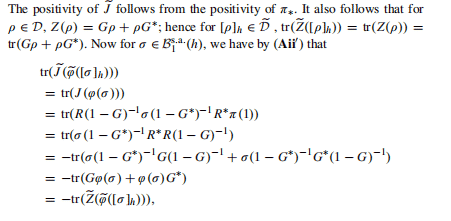
Note that $S_{t}$ and $\phi$ commute for each $t$, since $C_{t}^{}$ commutes with its generator $Y^{}$ and $C_{t}$ with $Y$. Now, using the perturbation expansion
$$
T_{, r}(\rho)=S_{, t}(\rho)+\int_{0}^{t} T_{*, t-s} \circ J \circ S_{s}(\rho) d s,
$$
we see that $T_{, t}(\rho) \geq S_{, t}(\rho)$ for positive $\rho$, and furthermore,
$$
\begin{aligned}
&\left|T_{, t}(\phi(\rho))-S_{, t}(\phi(\rho))\right|_{1} \
&\leq \int_{0}^{t}\left|T_{, t-s} \circ J \circ S_{, s}(\phi(\rho))\right|_{1} d s \
&\left.=\int_{0}^{t} | T_{, t-s} \circ J_{1} \circ S_{, s}(\rho)\right)\left|_{1} d s \leq 4 t\right| \rho |_{1}
\end{aligned}
$$

MATH 597U COURSE NOTES :
For a given completely positive map $T$ on $\mathcal{A}$, we formally define the Lindbladian
$$
\mathcal{L}=\sum_{k \in \mathbb{Z}^{d}} \mathcal{L}{k}, $$ where $$ \mathcal{L}{k}(x)=\tau_{k} \mathcal{L}{0}\left(\tau{-k} x\right) \text {, for all } x \in \mathcal{A},
$$
with
$$
\mathcal{L}{0}(x)=-\frac{1}{2}{T(1), x}+T(x) $$ and ${A, B}:=A B+B A$. In particular we consider the Lindbladian $\mathcal{L}$ for the completely positive map $$ T(x)=\sum{l=0}^{\infty} a(l)^{*} x a(l), \text { for all } x \in \mathcal{A},
$$