这是一份nottingham诺丁汉大学MATH2007作业代写的成功案例

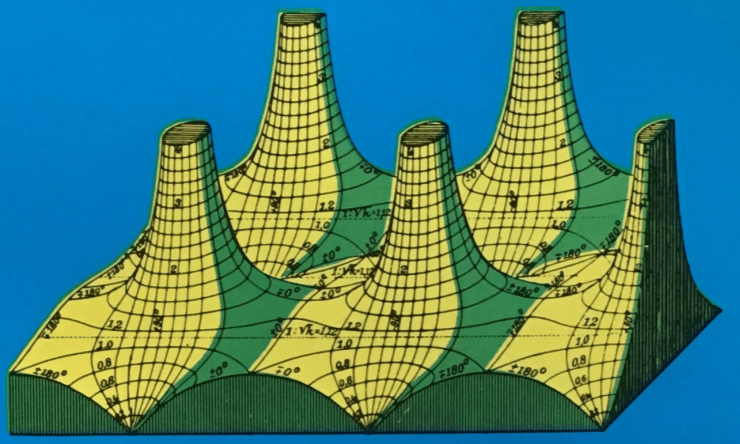
$\quad w=\sqrt{z}$.
In this $z=0$ is a branch-point. If we let the variable start from the point $z=1$ and describe the eireumference of a circle round the origin, this is a closed line which encloses the branch-point. If the fanction $w=\sqrt{z}$ start from the point $z=1$ with the value $w=+1$, and if we put
$$
z=r(\cos \phi+i \sin \phi),
$$
then at the point $z=1, r=1$ and $\phi=0$. If $z$ next describe the circumference of the circle in the direction of increasing angles, $r$ remains constant and equal to 1 , and $\phi$ inereases from 0 to $2 \pi$. If therefore the variable return to the point $z=1$, then
and therefore
$$
\begin{gathered}
z=\cos 2 \pi+i \sin 2 \pi, \
w=\sqrt{z}=\cos \pi+i \sin \pi=-1
\end{gathered}
$$

MATH2007 COURSE NOTES ：

$$
\sqrt[3]{\frac{z-a}{z-d} \cdot \frac{z-b}{z-e} \cdot \frac{(z-f)^{2}}{z^{2}}}
$$
by putting
$$
d=e=f=c .
$$
The branch-cuts can here also be chosen in a third way by drawing one from $a$ to 0 , and another from 0 to $b$.
The function
changes into
$$
\begin{aligned}
f(z) &=\sqrt[3]{(z-a)(z-b)} \
\phi(v) &=\sqrt[3]{\frac{(1-a u)(1-b u)}{u^{2}}}
\end{aligned}
$$