这是一份durham杜伦大学MATH41020-WE01作业代写的成功案例
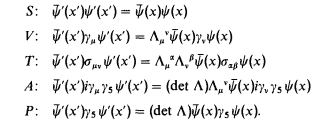

Velocity Transformation Matrix. In the language of transformation theory, postulate ii links time and space together by the four-vectors (note that this is not the convention used in most texts on general relativity)
$$
x_{\mu}=\left(x_{0}, \mathbf{x}\right), \quad x^{\mu}=\left(x_{0},-\mathbf{x}\right),
$$
where $x_{0}=t$ and $\mu=0,1,2,3$, such that the scalar product
$$
x_{\mu} x^{\mu}=x_{0}^{2}-\mathbf{x}^{2} \equiv x \cdot x=x^{2}
$$
is invariant from frame to frame,
$$
x_{\mu}^{\prime} x^{\prime \mu}=x_{\mu} x^{\mu} .
$$
Postulate $i$ then implies that there must exist a linear transformation connecting $x_{\mu}$ and $x_{\mu}^{\prime}$ obeying (3.3). For a passive Lorentz velocity transformation, $v_{x}=-v$, of an observer measuring an event at $x^{\prime}$ relative to an observer measuring the event at $x,(3.3)$ is satisfied provided (see Problem 3.1)
$$
\begin{aligned}
&t^{\prime}=\gamma(t+v x) \
&x^{\prime}=\gamma(x+v t), \quad y^{\prime}=y, \quad z^{\prime}=z
\end{aligned}
$$

MATH41020-WE01/MATH4061-WE01 COURSE NOTES :
we find
$$
\begin{aligned}
\Lambda_{\mu}{ }^{v} &=(\cosh \zeta I){\mu}{ }^{v}+(\sinh \zeta I){\mu}{ }^{v} \
&=\delta_{\mu}{ }^{v}-\left(I^{2}\right){\mu}{ }^{v}+\left(I^{2}\right){\mu}{ }^{v} \cosh \zeta+I_{\mu}{ }^{v} \sinh \zeta .
\end{aligned}
$$
Since (3.14) means $1-I^{2}$ is nonvanishing and unity only in the $y y$ and $z z$ entries, it is clear that (3.16) is identical to the original form of the velocity transformation (3.6) provided
$$
\gamma=\cosh \zeta, \quad \gamma v=\sinh \zeta,
$$
which implies $v=\tanh \zeta$ or $\gamma=\left(1-v^{2}\right)^{-\pm}$(see Problem 3.1). One can generalize (3.13)-(3.16) to include velocity transformations in an arbitrary direction by replacing $\zeta I_{\mu v}$ with the sum of three terms, one corresponding to each of the three space directions. It is also possible to invert (3.17) as
$$
\zeta=\tanh ^{-1} v=\frac{1}{2} \log \left(\frac{1+v}{1-v}\right),
$$