这是一份andrews圣安德鲁斯大学 MT2503作业代写的成功案例
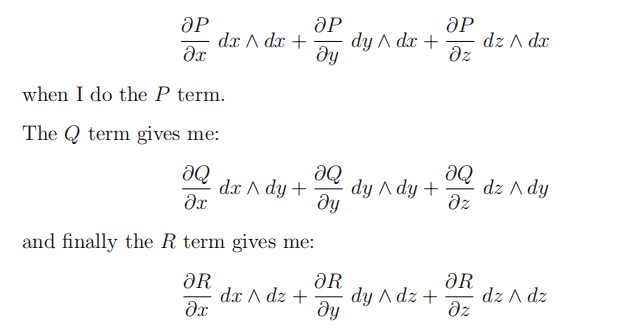

This tells us that provided the form is defined on all of $\mathbb{R}^{3}$, which it is, then it must be exact, and the corresponding vector field is conservative. So there must be a 0 -form $f$. We must have
$$
\frac{\partial f}{\partial x}=2 x y^{3} z^{4}
$$
so integrating with respect to $x$ we get
$$
x^{2} y^{3} z^{4}+u(y, z)
$$
for some unknown function of $y$ and $z$ only. Similar integration for the other two functions leads us to the conclusion that $u=\mathbf{0}$ and
$$
f(x, y, z)=x^{2} y^{3} z^{4}
$$

MT2503 COURSE NOTES :
Find an expression for the arc length of the graph of $y=x^{2}$ from the origin to the point $[1,1]^{T}$. Using Mathematica or otherwise, find the length of the curve.
Solution We can write the problem as $\int_{c} d \ell$ where $d \ell$ is an ‘infinitesimal’ bit of the curve. It is reasonable to write
$$
d \ell=\sqrt{(d x)^{2}+(d y)^{2}}
$$
Parametrise the curve by
$$
\left[\begin{array}{l}
x \
y
\end{array}\right]=\left[\begin{array}{c}
t \
t^{2}
\end{array}\right]
$$
Then note that the quantity $d \ell$ becomes just the norm of the differential term so we get:
$\int_{0}^{1}\left|\begin{array}{c}\dot{x}(t) \ \dot{y}(t)\end{array}\right| d t$
$=\int_{0}^{1} \sqrt{1+4 t^{2}} d t$