这是一份oxford牛津大学作业代写的成功案例
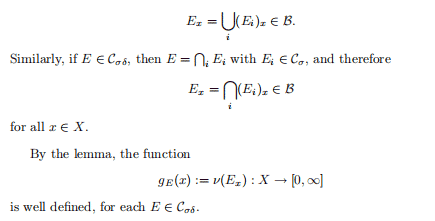

Proof. Case of real scalar field Take
$$
p(x):=\left|y^{}\right||x| \quad(x \in X) . $$ This function is subadditive and homogeneous, and $$ y^{} y \leq\left|y^{} y\right| \leq\left|y^{}\right||y|:=p(y) \quad(y \in Y)
$$
By Lemma 5.1, there exists a $p$-dominated linear functional $F$ on $X$ such that $\left.F\right|_{Y}=y^{*}$. Thus, for all $x \in X$,
$$
F(x) \leq\left|y^{}\right||x| $$ and $$ -F(x)=F(-x) \leq p(-x)=\left|y^{}\right||x|
$$
that is,
$$
|F(x)| \leq\left|y^{}\right||x| . $$ This shows that $F:=x^{} \in X^{}$ and $\left|x^{}\right| \leq\left|y^{}\right|$. Since the reversed inequality is trivial for any linear extension of $y^{}$, the theorem is proved in the case of real scalars.

Oxford COURSE NOTES :
$$
\psi:\left.x^{} \rightarrow x^{}\right|_{Y} \quad\left(x^{} \in X^{}\right)
$$
is a norm-decreasing linear map of $X^{}$ into $Y^{}$. For each $y^{* } \in Y^{ }$, the function $y^{ } \circ \psi$ belongs to $X^{ }$; we thus have the (continuous linear) map $$ \chi: Y^{ } \rightarrow X^{ } \quad \chi\left(y^{ }\right)=y^{ } \circ \psi . $$ Let $\kappa$ denote the canonical imbedding of $X$ onto $X^{ }$ (recall that $X$ is reflexive!), and consider the (continuous linear) map $$ \kappa^{-1} \circ \chi: Y^{ *} \rightarrow X
$$