这是一份UCL伦敦大学 MATH003701作业代写的成功案例
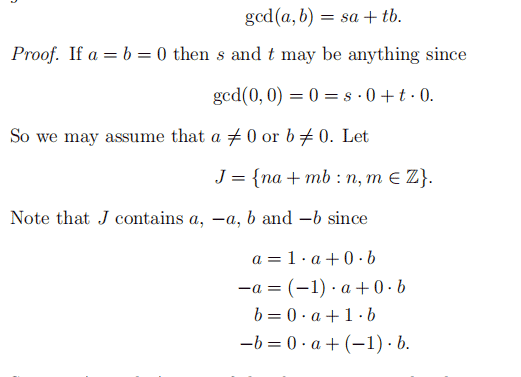

Proof. Assume, by way of contradiction, that there are only a finite number of prime numbers, say:
$$
p_{1}, p_{2}, \ldots, p_{n}
$$
Define
$$
N=p_{1} p_{2} \cdots p_{n}+1
$$
Since $p_{1} \geq 2$, clearly $N \geq 3$. So by Lemma $10.2 N$ has a prime divisor $p$. By assumption $p=p_{i}$ for some $i=1, \ldots, n$. Let $a=p_{1} \cdots p_{n}$. Note that
$$
a=p_{i}\left(p_{1} p_{2} \cdots p_{i-1} p_{i+1} \cdots p_{n}\right),
$$
so $p_{i} \mid a$. Now $N=a+1$ and by assumption $p_{i} \mid a+1$. So by Exercise $3.2$ $p_{i} \mid(a+1)-a$, that is $p_{i} \mid$

MATH003701 COURSE NOTES :
$$
a, a+1, a+2, \ldots, a+(n-1)
$$
are all composite.
Proof. Given $n \geq 1$ let $a=(n+1) !+2$. We claim that all the numbers
$$
a+i, \quad 0 \leq i \leq n-1
$$
composite. Since $(n+1) \geq 2$ clearly $2 \mid(n+1)$ ! and $2 \mid 2$. Hence $2 \mid(n+1) !+2$. Since $(n+1) !+2>2,(n+1) !+2$ is composite. Consider
$$
a+i=(n+1) !+i+2
$$