This module aims to provide an introduction to the ideas underlying the optimal choice of component variables, possibly subject to constraints, that maximise (or minimise) an objective function. The algorithms described are both mathematically interesting and applicable to a wide variety of complex real-life situations.
这是一份UCL伦敦大学学院STAT0025作业代写的成功案
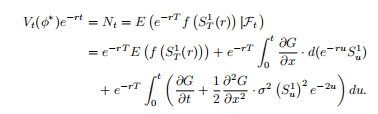
there is a flow of diffeomorphisms $x \rightarrow \xi_{s, t}(x)$ associated with this system, together with their non-singular Jacobians $D_{s, t}$.
In the terminology of Harrison and Pliska [150], the return process $Y_{t}=\left(Y_{t}^{1}, \ldots, Y_{t}^{d}\right)$ is here given by
$$
d Y_{t}=(\mu-\rho) d t+\Lambda d W_{t}
$$
can be removed by applying the Girsanov change of measure. Write
$$
\eta(t, S)=\Lambda(t, S)^{-1}(\mu(t, S)-\rho),
$$
and define the martingale $M$ by
$$
M_{t}=1-\int_{0}^{t} M_{s} \eta\left(s, S_{s}\right)^{\prime} d W_{s}
$$

STAT0025 COURSE NOTES :
Consider a standard Brownian motion $\left(B_{t}\right){t \geq 0}$ defined on $(\Omega, \mathcal{F}, P)$. The filtration $\left(\mathcal{F}{t}\right)$ is that generated by $B$. Recall that $B_{t}$ is normally distributed, and
$$
P\left(B_{t}<x\right)=\Phi\left(\frac{x}{\sqrt{t}}\right)
$$
Therefore
$$
P\left(B_{t} \geq x\right)=1-\Phi\left(\frac{x}{\sqrt{t}}\right)=\Phi\left(-\frac{x}{\sqrt{t}}\right)
$$
For a real-valued process $X$, we shall write
$$
M_{t}^{X}=\max {0 \leq s \leq t} X{s}, \quad m_{t}^{X}=\min {0 \leq s \leq t} X{s}
$$